Conjunto acotado en topología métrica
En un espacio métrico \((X, d)\), donde \(d\) es la métrica que mide la distancia entre puntos, un subconjunto \(A \subseteq X\) se dice acotado si existe un número positivo \(\mu > 0\) tal que, para cualesquiera dos puntos \(x, y \in A\), se cumple que \(d(x, y) \leq \mu\).
En términos sencillos, todos los puntos de \(A\) están contenidos dentro de una distancia máxima \(\mu\) entre sí.
Si el conjunto \(X\) completo resulta acotado con respecto a la métrica \(d\), se dice que \(d\) es una métrica acotada.
Esto implica que la distancia entre cualquier par de puntos de \(X\) está limitada por algún valor máximo \(\mu\).
Nota: Si la métrica \(d\) es acotada, entonces cualquier subconjunto de \(X\) también lo será, ya que sus distancias no pueden exceder las del conjunto total.
Un ejemplo práctico
Consideremos el plano cartesiano \(\mathbb{R}^2\) con la distancia euclidiana como métrica.
La distancia entre dos puntos \((x_1, y_1)\) y \((x_2, y_2)\) está dada por la fórmula:
$$ d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
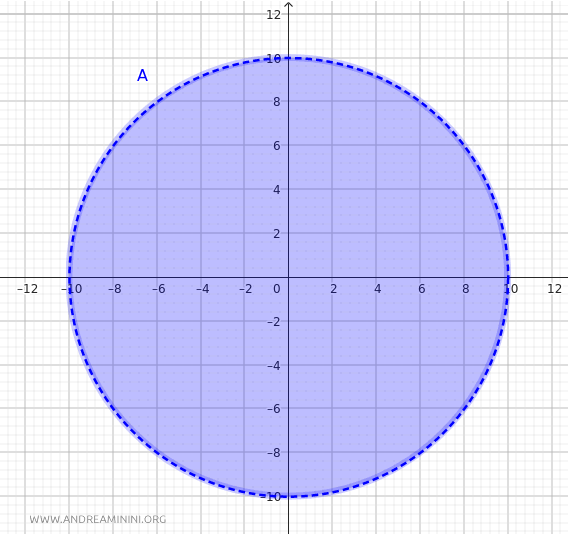
Tomemos ahora el subconjunto \(A\) de \(\mathbb{R}^2\), definido como el conjunto de todos los puntos \((x, y)\) que satisfacen la ecuación de un círculo de radio \(10\), centrado en el origen. Este conjunto se describe como:
$$ A = \{(x, y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 10^2\} $$
Un conjunto es acotado si existe un valor \(\mu > 0\) tal que, para todo par de puntos \((x_1, y_1), (x_2, y_2) \in A\), se cumple que \(d((x_1, y_1), (x_2, y_2)) \leq \mu\).
En este caso, la mayor distancia posible entre dos puntos de \(A\) se alcanza cuando se sitúan en extremos opuestos del diámetro del círculo (por ejemplo, \((10, 0)\) y \((-10, 0)\)).
La distancia entre dichos puntos es:
$$ d((10, 0), (-10, 0)) = \sqrt{((-10) - 10)^2 + (0 - 0)^2} = \sqrt{(-20)^2} = 20 $$
Así pues, la distancia máxima entre puntos de \(A\) es \(20\).
Esto significa que, sin importar qué dos puntos elijamos dentro del círculo, su distancia nunca superará las \(20\) unidades.
En consecuencia, el conjunto \(A\) es acotado con \(\mu = 20\), ya que todos sus puntos se encuentran dentro de una distancia máxima, que coincide con el diámetro del círculo.
La acotación de una métrica no afecta la topología
Conviene subrayar que el hecho de que una métrica sea acotada o no, no modifica la topología que induce, es decir, la estructura de los conjuntos abiertos y cerrados.
¿Qué es la topología? La topología es el marco que permite definir qué conjuntos se consideran “abiertos” o “cerrados”. No depende de los valores concretos de la métrica, sino de cómo se organiza el espacio a nivel estructural.
Por ello, aunque una métrica no sea acotada, siempre es posible encontrar otra métrica equivalente que sí lo sea y que genere exactamente la misma topología.
En otras palabras: que una métrica esté acotada o no, no altera la definición de los conjuntos abiertos o cerrados dentro del espacio.
Ejemplo
Para convertir una métrica no acotada en una acotada, se puede aplicar una función matemática que “comprime” las distancias grandes sin modificar la estructura topológica del espacio.
Un método habitual consiste en usar la siguiente transformación:
$$ d'(x, y) = \frac{d(x, y)}{1 + d(x, y)} $$
¿Cómo actúa esta transformación?
Cuando la distancia \(d(x, y)\) es pequeña, \(d'(x, y)\) se aproxima mucho a \(d(x, y)\).
Por ejemplo, si \(d(x, y) = 1\), entonces la distancia transformada es:
$$ d'(x, y) = \frac{1}{1 + 1} = 0.5 $$
Cuando \(d(x, y)\) es muy grande (tiende a infinito), la nueva distancia \(d'(x, y)\) tiende a \(1\).
Así, sin importar cuán grandes sean las distancias originales, la transformación garantiza que todas queden dentro del intervalo \([0, 1)\).
Por ejemplo, consideremos un espacio métrico \((X, d)\) donde la distancia se define como \(d(x, y) = |x - y|\) (la métrica euclidiana usual).
Esta métrica no es acotada, ya que los puntos \(x\) e \(y\) pueden estar arbitrariamente lejos.
Si aplicamos la transformación, obtenemos:
$$ d'(x, y) = \frac{|x - y|}{1 + |x - y|} $$
Si \(x = 1\) e \(y = 2\), la distancia original es \(d(1, 2) = 1\), y la transformada resulta:
$$ d'(1, 2) = \frac{1}{1 + 1} = 0.5 $$
Si \(x = 1\) e \(y = 1000\), la distancia original es \(d(1, 1000) = 999\), y la transformada es:
$$ d'(1, 1000) = \frac{999}{1 + 999} = 0.999 $$
Como resultado, todas las distancias quedan dentro del intervalo \([0, 1)\).
La estructura topológica del espacio permanece intacta, ya que los conjuntos abiertos y cerrados definidos por \(d\) y \(d'\) coinciden exactamente.
Y así sucesivamente.