Ejemplo Resuelto - Análisis de Funciones 6

En este ejemplo vamos a estudiar la siguiente función y a construir su gráfica:

$$ f(x) = x^3 - 3x + 2 $$

Aplicaremos las técnicas habituales del análisis matemático para describir su comportamiento.

Dominio

El dominio de la función coincide con el conjunto de todos los números reales:

$$ D_f = \mathbb{R} $$

La función está definida para cualquier valor real de $ x $.

Intersecciones

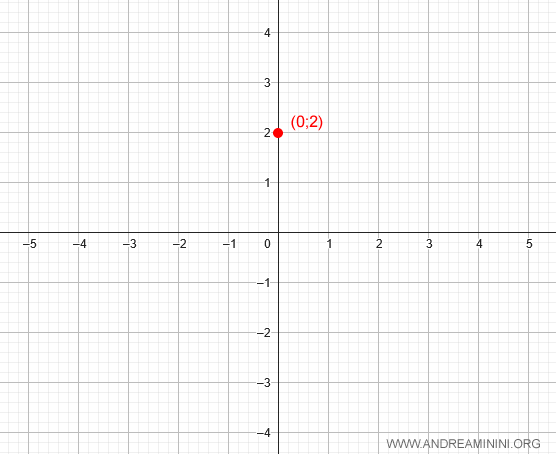
Para determinar la intersección con el eje y, evaluamos la función en $ x = 0 $:

$$ y = 0^3 - 3 \cdot 0 + 2 = 2 $$

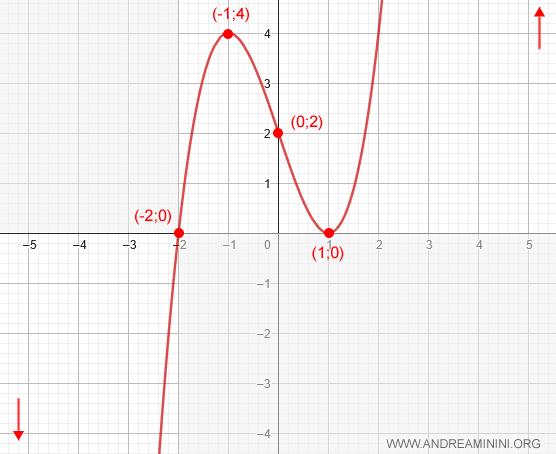
Por tanto, la gráfica pasa por el punto (0, 2):

la función pasa por el punto (0, 2)

Para encontrar las intersecciones con el eje x, resolvemos:

$$ x^3 - 3x + 2 = 0 $$

Es inmediato comprobar que $ x = 1 $ es una raíz. Podemos entonces factorizar el polinomio mediante el método de Ruffini:

$$ \begin{array}{c|lcc|r} & 1 & 0 & -3 & 2 \\ 1 & & 1 & 1 & -2 \\ \hline & 1 & 1 & -2 & 0 \end{array} $$

Obtenemos la factorización:

$$ (x - 1)(x^2 + x - 2) $$

El primer factor se anula en $ x = 1 $. El segundo corresponde a una cuadrática cuyas raíces son:

$$ x = \frac{-1 \pm \sqrt{1 - 4(1)(-2)}}{2} $$

$$ x = \frac{-1 \pm \sqrt{9}}{2} $$

$$ x = \frac{-1 \pm 3}{2} $$

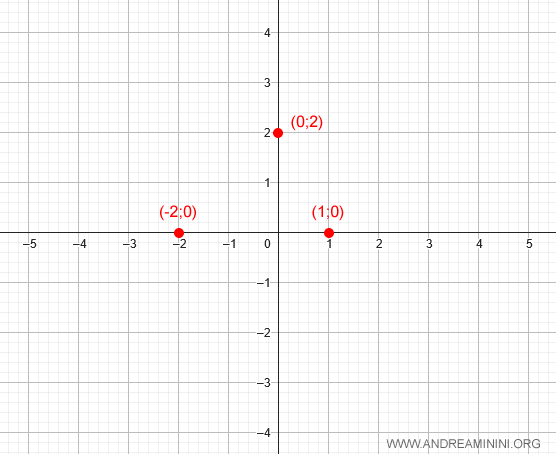
$$ x = \begin{cases} \frac{-1 - 3}{2} = -2 \\[6pt] \frac{-1 + 3}{2} = 1 \end{cases} $$

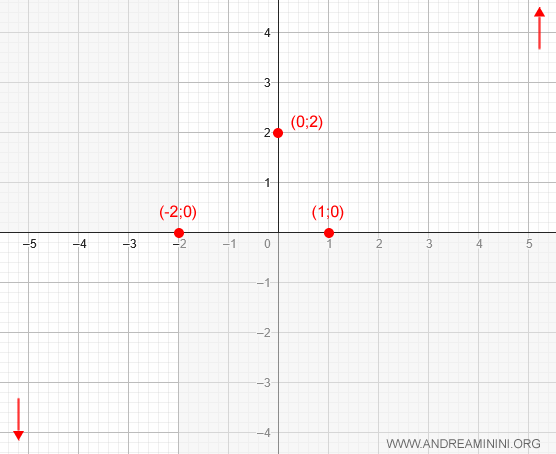
Por lo tanto, la función corta el eje x en $ x = -2 $ y en $ x = 1 $, pasando por los puntos (-2, 0) y (1, 0):

la función corta el eje x en x = -2 y x = 1

Asíntotas

Dado que la función está definida en todo su dominio, no existen asíntotas verticales.

Para comprobar la existencia de asíntotas horizontales, estudiamos los límites en el infinito:

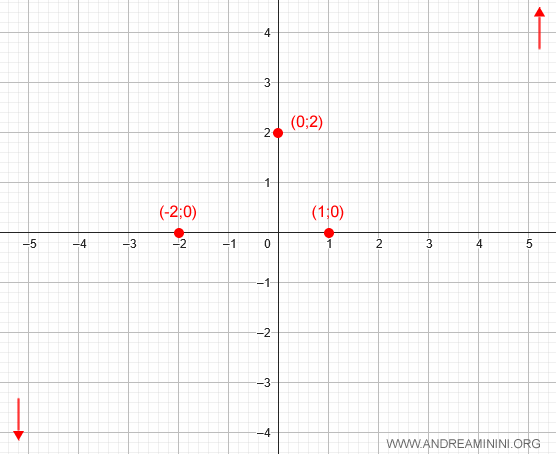
$$ \lim_{x \rightarrow +\infty} (x^3 - 3x + 2) = +\infty $$

$$ \lim_{x \rightarrow -\infty} (x^3 - 3x + 2) = -\infty $$

Concluimos que no hay asíntotas horizontales: la función tiende a $ +\infty $ cuando $ x \to +\infty $ y a $ -\infty $ cuando $ x \to -\infty $.

Este comportamiento en los extremos puede marcarse en la gráfica como referencia:

comportamiento en el infinito

Análisis de signos

Para estudiar el signo de la función utilizamos la factorización obtenida:

$$ f(x) = (x - 1)(x^2 + x - 2) $$

Esto facilita el análisis:

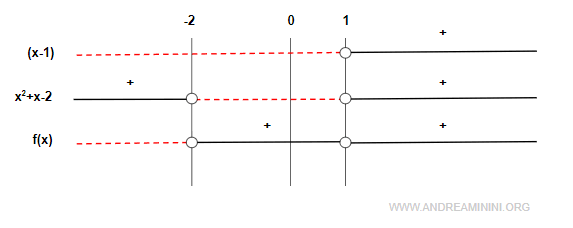
análisis de signos de la función

El factor $ (x - 1) $ es positivo cuando $ x > 1 $. El cuadrático corresponde a una parábola que se abre hacia arriba, con raíces en $ x = -2 $ y $ x = 1 $.

De este modo, la función resulta negativa en (-∞, -2) y positiva en (-2, ∞).

Podemos excluir en la gráfica las regiones del plano donde la función no toma valores:

análisis de signos

Crecimiento y decrecimiento

Calculemos la primera derivada para identificar los intervalos de crecimiento y decrecimiento:

$$ f'(x) = D_x[x^3 - 3x + 2] = 3x^2 - 3 $$

Resolvemos la condición $ f'(x) > 0 $:

$$ x^2 > 1 $$

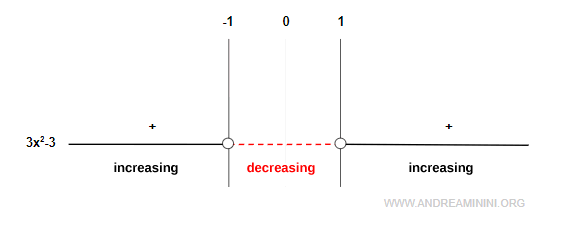
Por tanto, $ f'(x) $ es positiva en (-∞, -1) y (1, ∞), y se anula en $ x = -1 $ y $ x = 1 $:

signo de la primera derivada

De aquí se deduce:

La función es creciente en (-∞, -1)
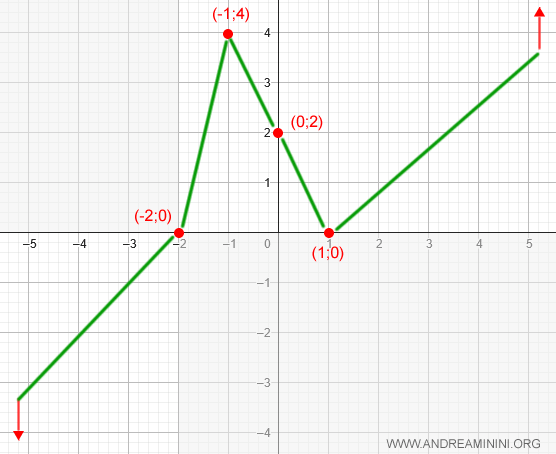
En $ x = -1 $ se localiza un máximo, pues $ f'(x) = 0 $ y la función pasa de creciente a decreciente.
Nota. Coordenadas: $$ y = (-1)^3 - 3(-1) + 2 = -1 + 3 + 2 = 4 $$ Máximo local en (-1, 4).
La función es decreciente en (-1, 1)
En $ x = 1 $ se localiza un mínimo, ya que $ f'(x) = 0 $ y la función pasa de decreciente a creciente.
Nota. Coordenadas: $$ y = (1)^3 - 3(1) + 2 = 1 - 3 + 2 = 0 $$ Mínimo local en (1, 0).
La función es creciente en (1, ∞)

Esta información puede incorporarse a la representación gráfica:

gráfica de la función

Concavidad y convexidad

Analizamos ahora la curvatura calculando la segunda derivada:

$$ f''(x) = D_x[3x^2 - 3] = 6x $$

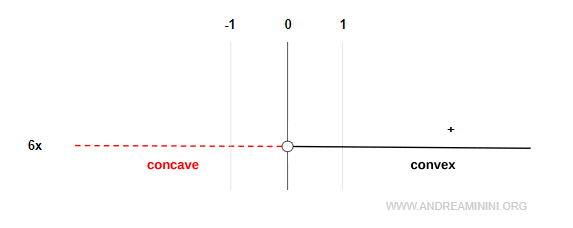
La segunda derivada es negativa en (-∞, 0) y positiva en (0, ∞):

signo de la segunda derivada

Por lo tanto:

La función es cóncava en (-∞, 0)
La función es convexa en (0, ∞)

Con esta última información obtenemos la forma definitiva de la gráfica:

gráfica final de la función

De este modo queda completado el análisis.