Ejemplo resuelto de análisis de funciones 5

En este ejemplo analizaremos la siguiente función y trazaremos su gráfica:

$$ f(x) = \frac{x}{1-x} $$

Se trata de una función racional.

Puntos de indefinición

Primero identificamos los valores de $x$ para los que la función no está definida:

$$ 1 - x = 0 $$

$$ x = 1 $$

La función no existe en $x = 1$, ya que el denominador se anula y la división por cero no está definida.

Dominio de la función

Por lo tanto, el dominio está formado por todos los números reales salvo $x = 1$:

$$ D_f = (-\infty, 1) \cup (1, \infty) $$

Intersecciones con los ejes

En $x = 0$, la función toma el valor:

$$ f(0) = \frac{0}{1-0} = 0 $$

La gráfica pasa, por tanto, por el origen $O = (0,0)$:

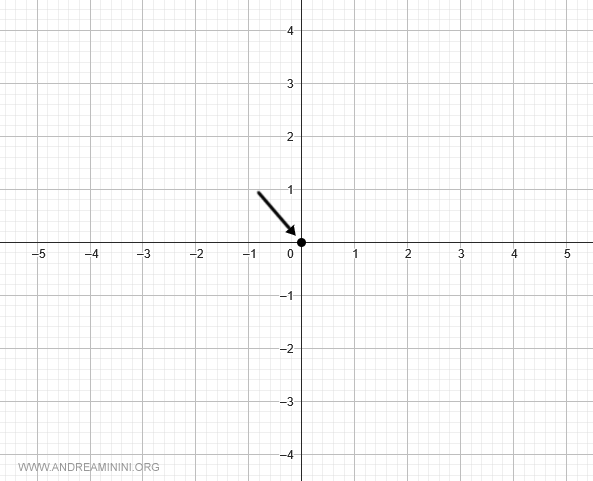
Análisis del signo

Estudiemos ahora el signo de la función:

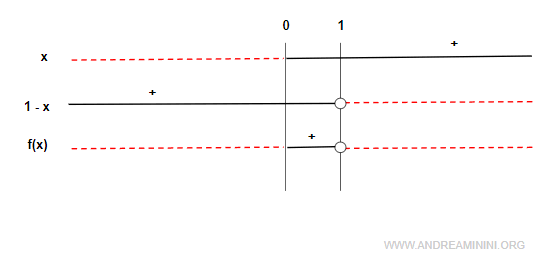
Dentro de su dominio, $f(x)$ es positiva en el intervalo $(0,1)$, nula en $x = 0$ y negativa en el resto.

Con esta información podemos marcar las regiones principales en el plano cartesiano:

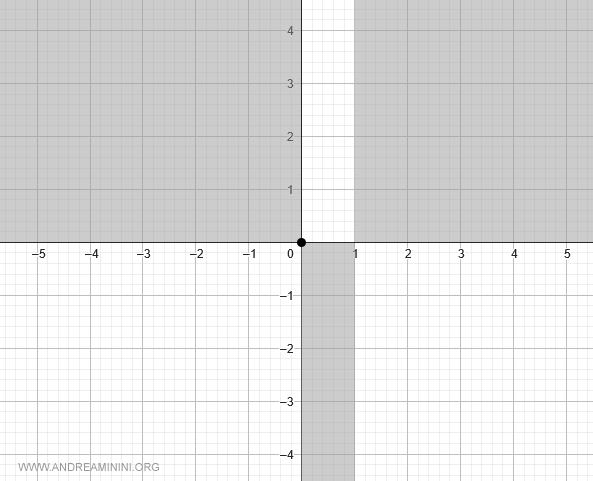
Asíntotas horizontales

Analicemos ahora el comportamiento de la función cuando $x$ tiende a $+\infty$:

$$ \lim_{x \rightarrow +\infty} \frac{x}{1-x} = \frac{\infty}{-\infty} $$

Se trata de una forma indeterminada del tipo ∞/∞, que resolvemos aplicando la regla de L'Hôpital:

$$ \lim_{x \rightarrow +\infty} \frac{D[x]}{D[1-x]} = \frac{1}{-1} = -1 $$

Por lo tanto, cuando $x \to +\infty$, la función se aproxima a la recta $y = -1$:

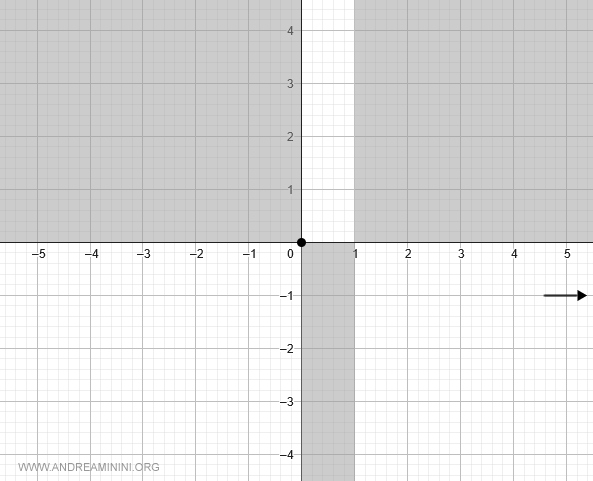
De forma análoga, para $x \to -\infty$:

$$ \lim_{x \rightarrow -\infty} \frac{x}{1-x} = \frac{-\infty}{\infty} $$

Aplicamos nuevamente la regla de L'Hôpital:

$$ \lim_{x \rightarrow -\infty} \frac{D[x]}{D[1-x]} = \frac{1}{-1} = -1 $$

Así, cuando $x \to -\infty$, la función también se aproxima a $y = -1$:

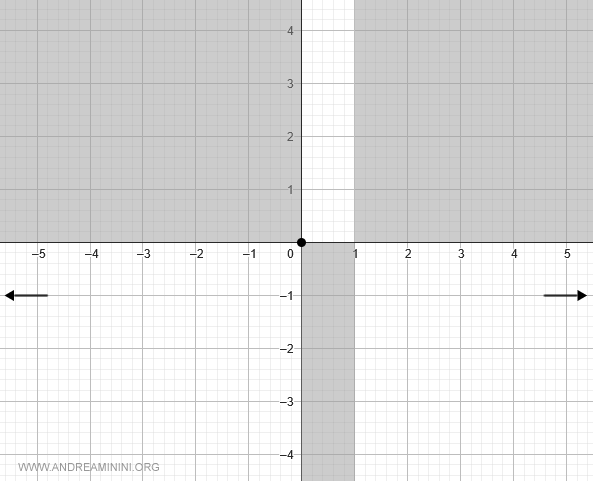
En conclusión, la función posee una asíntota horizontal en $y = -1$:

 

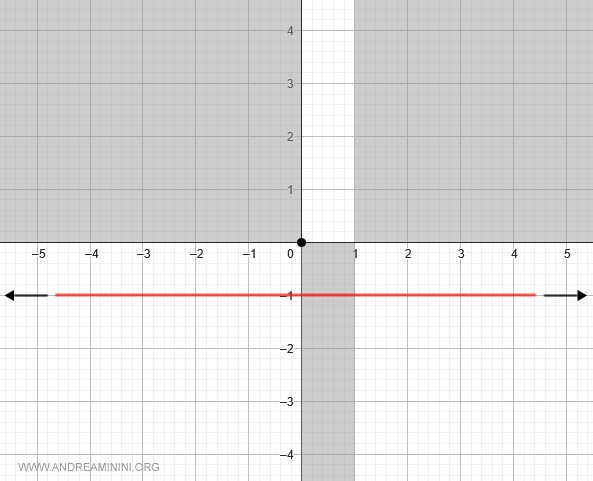
Asíntotas verticales

Las asíntotas verticales aparecen en los puntos donde la función no está definida; en este caso, en $x = 1$.

Si nos aproximamos por la derecha:

$$ \lim_{x \rightarrow 1^+} \frac{x}{1-x} = -\infty $$

Lo representamos en la gráfica:

 

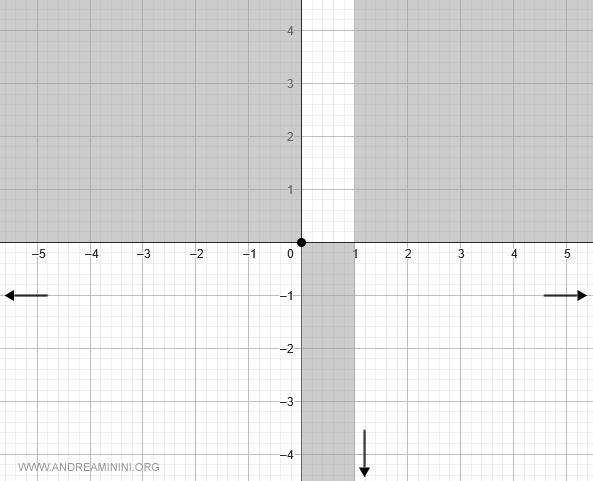
Si nos aproximamos por la izquierda:

$$ \lim_{x \rightarrow 1^-} \frac{x}{1-x} = +\infty $$

También visible en la gráfica:

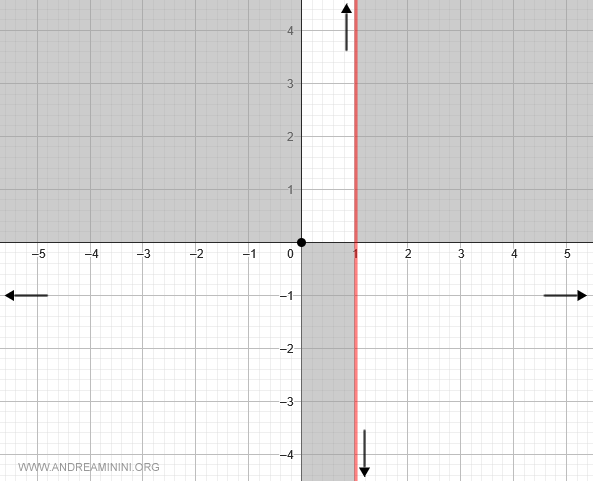
Intervalos de crecimiento y decrecimiento

Para determinar en qué intervalos la función crece o decrece, calculamos su primera derivada:

$$ f'(x) = D\left[ \frac{x}{1-x} \right] $$

Aplicamos la regla del cociente:

Nota. La derivada de un cociente es: $$ \frac{f'(x)g(x) - f(x)g'(x)}{[g(x)]^2} $$

$$ f'(x) = \frac{1 \cdot (1-x) - x \cdot (-1)}{(1-x)^2} $$

$$ f'(x) = \frac{1 - x + x}{(1-x)^2} $$

Por lo tanto:

$$ f'(x) = \frac{1}{(1-x)^2} $$

El numerador es siempre positivo y el denominador, al estar al cuadrado, también. En consecuencia, $f'(x) > 0$ para todo $x$ en el dominio:

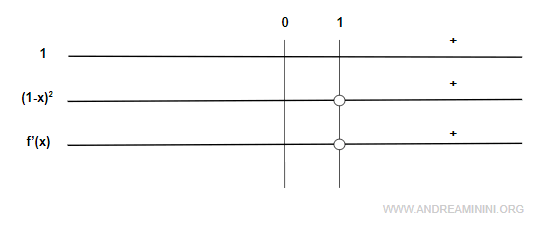
De ello se sigue que la función es estrictamente creciente en todo su dominio.

Además, dado que $f'(x) \ne 0$, no presenta máximos ni mínimos locales.

Podemos completar la gráfica con esta información:

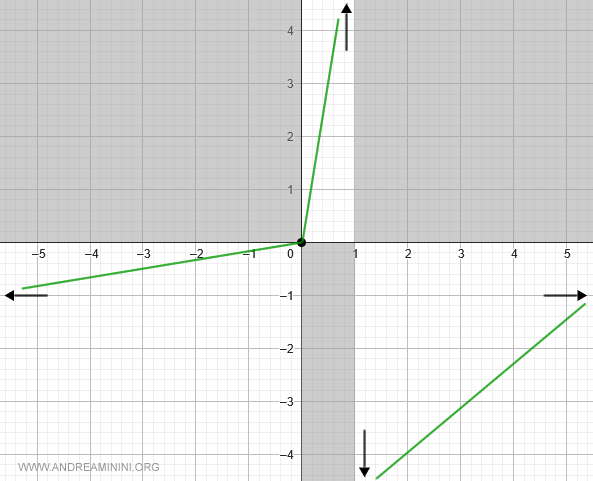
Concavidad y convexidad

Para analizar la curvatura de la gráfica calculamos la segunda derivada:

$$ f''(x) = D\left[ \frac{1}{(1-x)^2} \right] $$

$$ f''(x) = \frac{2}{(1-x)^3} $$

Examinemos ahora el signo de $f''(x)$:

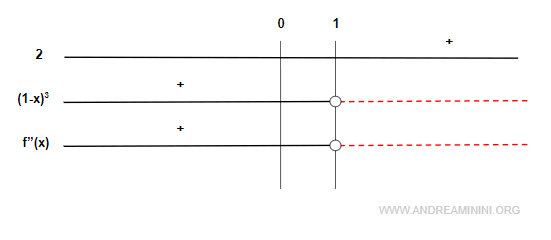
De aquí obtenemos la información final necesaria para caracterizar la gráfica:

• Si $f''(x) > 0$ en $(-\infty, 1)$, la función es convexa en ese intervalo.
• Si $f''(x) < 0$ en $(1, +\infty)$, la función es cóncava en ese intervalo.

La representación final de la función es la siguiente:

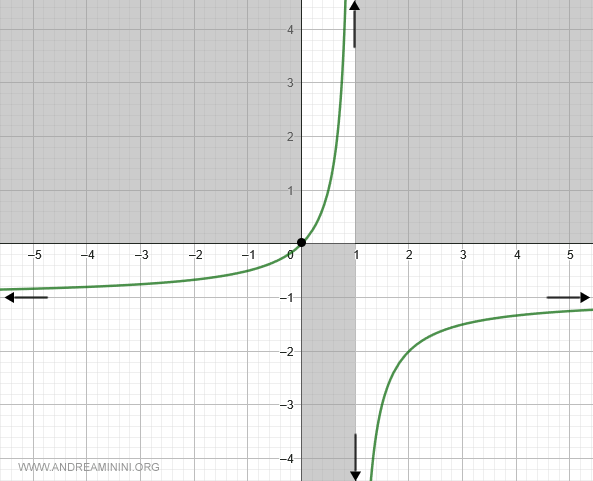
Con esto se completa el análisis.