Ejercicio de análisis de funciones 10

En este ejercicio vamos a estudiar la función exponencial aplicando las técnicas clásicas del cálculo diferencial:

$$ f(x)= e^{- \frac{1}{x}} $$

Dominio

La función está definida para todos los números reales, excepto en $ x = 0 $:

$$ D_f = \mathbb{R} \setminus \{ 0 \} $$

La exclusión de este punto se debe a que el exponente $ \frac{1}{x} $ no está definido en cero, ya que implica una división por cero.

Intersecciones

Analicemos ahora si la curva llega a cortar alguno de los ejes coordenados:

Intersección con el eje y
Como la función no está definida en $ x = 0 $, no existe intersección con el eje y.
Intersección con el eje x
Para comprobar si la gráfica corta el eje x, resolvemos: $$ f(x) = 0 \;\;\Rightarrow\;\; e^{- \frac{1}{x}} = 0 $$ Aplicamos logaritmo natural en ambos miembros: $$ \ln\left(e^{- \frac{1}{x}}\right) = \ln(0) $$ $$ -\frac{1}{x} = \ln(0) $$ Pero como $ \ln(0) $ no está definido, la ecuación carece de solución. En consecuencia, la función no corta el eje x.

Conclusión: la función no presenta intersecciones con ninguno de los ejes.

Signo

La determinación del signo resulta inmediata: la función exponencial es siempre positiva, de modo que:

$$ f(x) = e^{- \frac{1}{x}} > 0 \quad \forall x \in D_f $$

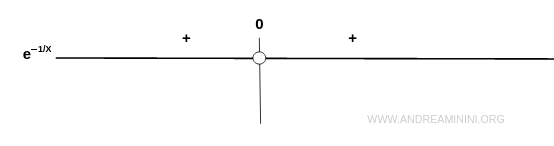
la función es siempre positiva

De ello se sigue que la gráfica permanece completamente en los cuadrantes primero y segundo del plano cartesiano.

borrador inicial de la gráfica

Asíntotas verticales

Estudiemos el comportamiento de la función en la discontinuidad de $ x = 0 $:

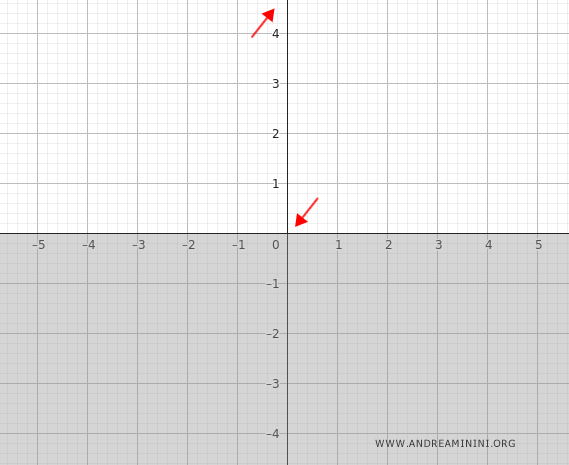
Cuando $ x \to 0^- $, el exponente $ -\frac{1}{x} \to +\infty $, y por tanto:

$$ \lim_{x \to 0^-} e^{- \frac{1}{x}} = \infty $$

Cuando $ x \to 0^+ $, ocurre que $ -\frac{1}{x} \to -\infty $, y por consiguiente:

$$ \lim_{x \to 0^+} e^{- \frac{1}{x}} = 0 $$

Dado que los límites laterales son distintos, la función presenta una discontinuidad en $ x = 0 $, pero no existe una asíntota vertical en ese punto.

comportamiento de la función cerca de x = 0

Asíntotas horizontales

Consideremos ahora el comportamiento cuando $ x \to \pm \infty $:

Para $ x \to +\infty $:

$$ \lim_{x \to +\infty} e^{- \frac{1}{x}} = \frac{1}{e^{\frac{1}{x}}} \;\;\to\;\; \frac{1}{1} = 1^- $$

Explicación: al crecer $ x $, se cumple $ \frac{1}{x} \to 0^+ $. Como $ e^{\frac{1}{x}} > 1 $, resulta $ \frac{1}{e^{1/x}} < 1 $, es decir, la función se aproxima a 1 desde abajo.

Para $ x \to -\infty $:

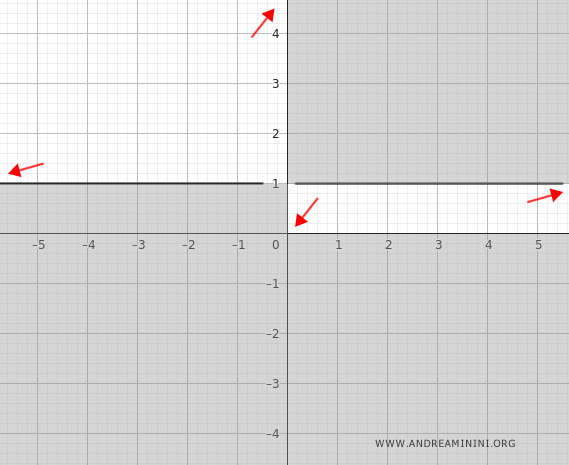
$$ \lim_{x \to -\infty} e^{- \frac{1}{x}} = \frac{1}{e^{\frac{1}{x}}} \;\;\to\;\; \frac{1}{1} = 1^+ $$

Explicación: en este caso, $ \frac{1}{x} \to 0^- $. Como $ e^{\frac{1}{x}} < 1 $, se obtiene $ \frac{1}{e^{1/x}} > 1 $, de modo que la función se aproxima a 1 desde arriba.

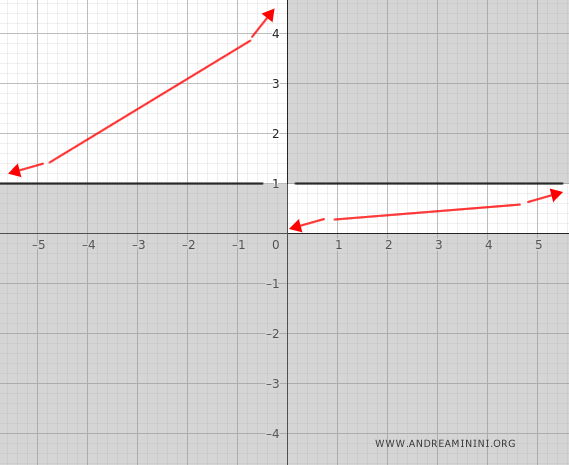
Conclusión: la función tiene una asíntota horizontal en $ y = 1 $.

gráfica con asíntota horizontal

Monotonía

Para determinar en qué intervalos la función crece o decrece, calculamos la primera derivada:

$$ f'(x) = \frac{d}{dx} \left( e^{- \frac{1}{x}} \right) = e^{- \frac{1}{x}} \cdot \frac{1}{x^2} $$

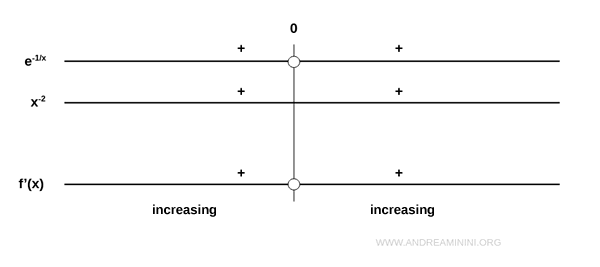
signo de la primera derivada

Ambos factores son estrictamente positivos, por lo que $ f'(x) > 0 $ en todo el dominio.

En consecuencia, la función es estrictamente creciente en todo $ x \in D_f $.

comportamiento creciente de la gráfica

Concavidad y puntos de inflexión

Examinemos ahora la concavidad a partir del cálculo de la segunda derivada:

$$ f''(x) = \frac{d}{dx} \left( x^{-2} \cdot e^{- \frac{1}{x}} \right) $$

Aplicamos la regla del producto:

$$ f''(x) = -2x^{-3} \cdot e^{- \frac{1}{x}} + x^{-2} \cdot \left( \frac{1}{x^2} \cdot e^{- \frac{1}{x}} \right) $$

$$ f''(x) = e^{- \frac{1}{x}} \cdot \left( -2x^{-3} + x^{-4} \right) $$

Reordenando términos:

$$ f''(x) = e^{- \frac{1}{x}} \cdot x^{-3} \cdot \left( -2 + \frac{1}{x} \right) $$

$$ f''(x) = e^{- \frac{1}{x}} \cdot \frac{1 - 2x}{x^4} $$

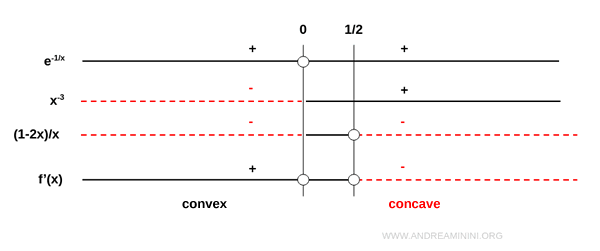
signo de la segunda derivada

Nota: el signo de la segunda derivada depende de la fracción $ \frac{1 - 2x}{x} $. Es positiva cuando $ 0 < x < \frac{1}{2} $.

De este estudio se deduce:

La función es cóncava hacia arriba (convexa) en $ (-\infty, \frac{1}{2}) $
La función es cóncava hacia abajo en $ (\frac{1}{2}, +\infty) $

En $ x = \frac{1}{2} $ la concavidad cambia de signo, lo que señala la presencia de un punto de inflexión.

Con esta información, ya podemos completar la representación gráfica de la función:

gráfico completo de la función

Con esto concluye el análisis.