Ejercicio de análisis de funciones 7
En este ejercicio vamos a estudiar la función exponencial
$$ e^x + e^{-x} $$
Comenzaremos determinando su dominio.
Dominio
Para precisar el dominio, reescribamos la función en una forma algebraicamente más manejable:
$$ f(x) = e^x + e^{-x} $$
$$ f(x) = e^x + \frac{1}{e^x} $$
$$ f(x) = \frac{e^x \cdot e^x + 1}{e^x} $$
$$ f(x) = \frac{e^{2x} + 1}{e^x} $$
Hemos obtenido así una expresión racional. Como la función exponencial nunca se anula y siempre es positiva, el denominador no presenta problemas. Por lo tanto, la función está bien definida para cualquier número real.
En conclusión, el dominio es todo el conjunto de los números reales:
$$ D_f = \mathbb{R} $$
Análisis del signo
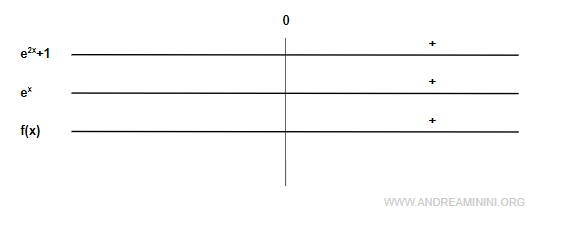
La función \( f(x) = \frac{e^{2x} + 1}{e^x} \) resulta estrictamente positiva en todo \( \mathbb{R} \), puesto que tanto el numerador como el denominador son siempre mayores que cero.
Intersecciones con los ejes
Del análisis anterior sabemos que la función nunca se anula, por lo que no corta el eje x. No obstante, para mayor rigor, confirmémoslo analíticamente.
Planteamos la ecuación \( f(x) = 0 \):
$$ \frac{e^{2x} + 1}{e^x} = 0 $$
Multiplicamos ambos miembros por \( e^x \):
$$ e^{2x} + 1 = 0 $$
$$ e^{2x} = -1 $$
Pero esta ecuación no tiene solución en los números reales, ya que la función exponencial es siempre positiva y nunca puede ser igual a un valor negativo.
En consecuencia, la función no presenta intersecciones con el eje x.
Intersección con el eje y
Para hallar la intersección con el eje y, evaluamos la función en \( x = 0 \):
$$ f(x) = \frac{e^{2x} + 1}{e^x} $$
$$ f(0) = \frac{e^0 + 1}{e^0} = \frac{1 + 1}{1} = 2 $$
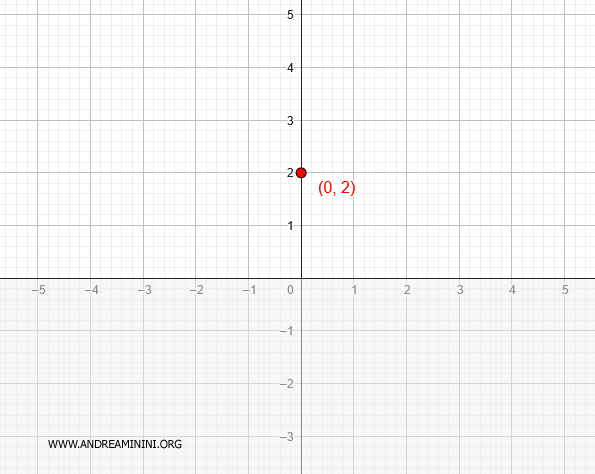
Por lo tanto, la gráfica corta el eje y en el punto \( (0, 2) \).
Este resultado proporciona un punto de referencia fundamental para la construcción de la curva.
Asíntotas
La función es continua y está definida en todo su dominio, por lo que no existen asíntotas verticales.
Para comprobar si aparecen asíntotas horizontales, estudiemos los límites cuando \( x \to \pm\infty \):
Si \( x \to +\infty \):
$$ \lim_{x \to \infty} \left(e^x + e^{-x}\right) = \infty + 0 = \infty $$
Si \( x \to -\infty \):
$$ \lim_{x \to -\infty} \left(e^x + e^{-x}\right) = 0 + \infty = \infty $$
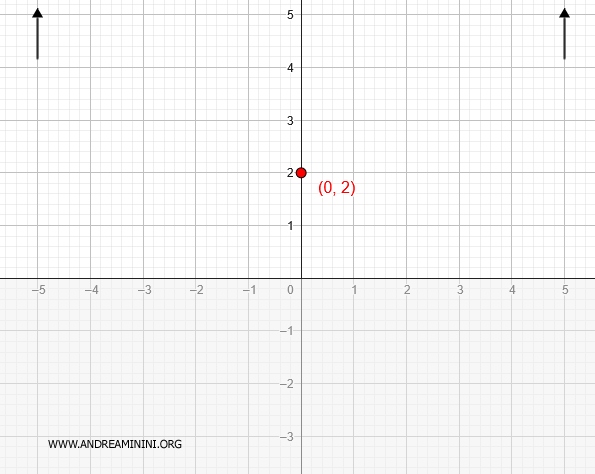
En ambos casos la función diverge, por lo que no posee asíntotas horizontales.
Intervalos de crecimiento y decrecimiento
Para determinar en qué intervalos la función es creciente o decreciente, calculamos la primera derivada y estudiamos su signo.
Usando la forma simplificada \( f(x) = e^x + e^{-x} \):
$$ f'(x) = \frac{d}{dx}(e^x) + \frac{d}{dx}(e^{-x}) = e^x - e^{-x} $$
Nota: con la forma racional se llega al mismo resultado, aunque con un procedimiento más largo: $$ f'(x) = \frac{d}{dx}\left(\frac{e^{2x} + 1}{e^x}\right) $$ Aplicamos la regla del cociente: $$ f'(x) = \frac{(2e^{2x}) \cdot e^x - (e^{2x} + 1) \cdot e^x}{(e^x)^2} $$ $$ = \frac{2e^{3x} - e^{3x} - e^x}{e^{2x}} = \frac{e^{3x} - e^x}{e^{2x}} $$ Al factorizar y simplificar: $$ = \frac{e^x(e^{2x} - 1)}{e^{2x}} = \frac{e^{2x} - 1}{e^x} $$
Así, podemos expresar la derivada como:
$$ f'(x) = \frac{e^{2x} - 1}{e^x} $$
El numerador es negativo para \( x < 0 \) y positivo para \( x > 0 \), mientras que el denominador es siempre positivo.
De ello se deduce:
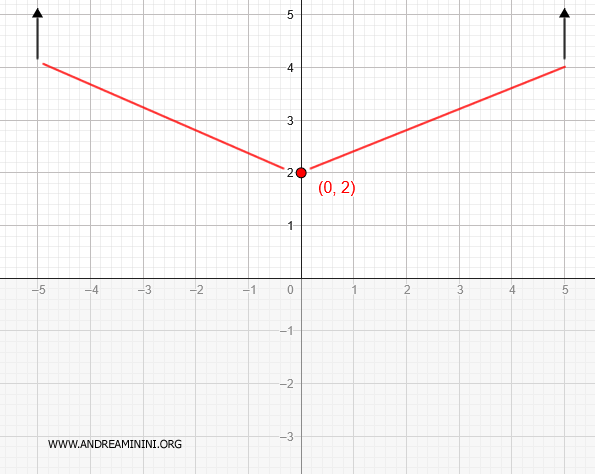
- En \( (-\infty, 0) \) la derivada es negativa → la función es decreciente
- En \( (0, \infty) \) la derivada es positiva → la función es creciente
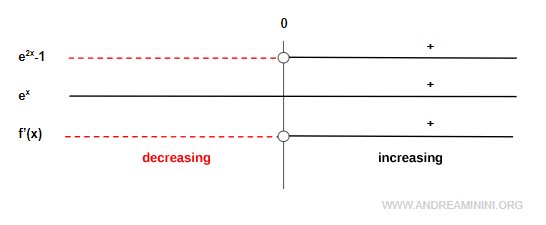
Incorporamos ahora esta información en la representación gráfica.
Extremos locales
Los puntos críticos se obtienen donde la primera derivada se anula:
$$ f'(x) = 0 \;\;\Rightarrow\;\; e^x = e^{-x} $$
Aplicando logaritmos naturales en ambos lados: $$ \log(e^x) = \log(e^{-x}) \;\;\Rightarrow\;\; x = -x \;\;\Rightarrow\;\; 2x = 0 \;\;\Rightarrow\;\; x = 0 $$
Por lo tanto, \( x = 0 \) es un punto crítico.
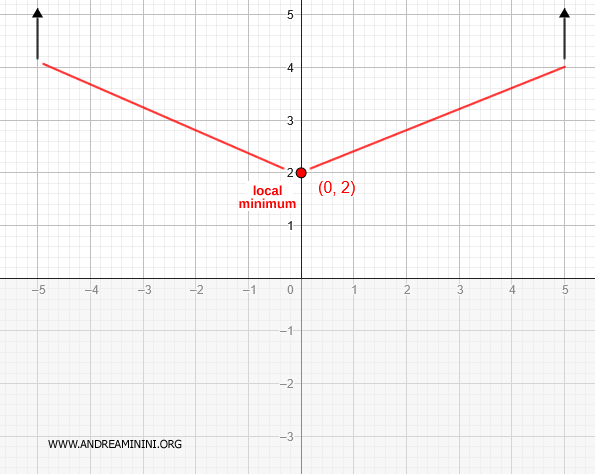
Como la función pasa de decreciente a creciente en este punto, se trata de un mínimo local.

Evaluando la función en ese valor:
$$ f(0) = e^0 + e^0 = 1 + 1 = 2 $$
Así pues, la función posee un mínimo local en el punto (0, 2).
Concavidad y convexidad
Para estudiar la curvatura de la función calculamos la segunda derivada a partir de la forma más simple:
$$ f''(x) = \frac{d}{dx}(e^x - e^{-x}) = e^x + e^{-x} $$
Que puede reescribirse también como:
$$ f''(x) = \frac{e^{2x} + 1}{e^x} $$
Esta expresión es siempre estrictamente positiva para todo número real.
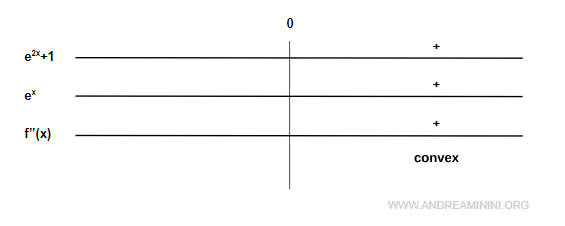
En consecuencia, la función es estrictamente convexa en todo su dominio, sin presentar puntos de inflexión.
Con todos estos resultados disponemos ya de una descripción completa de la función y de su gráfica.
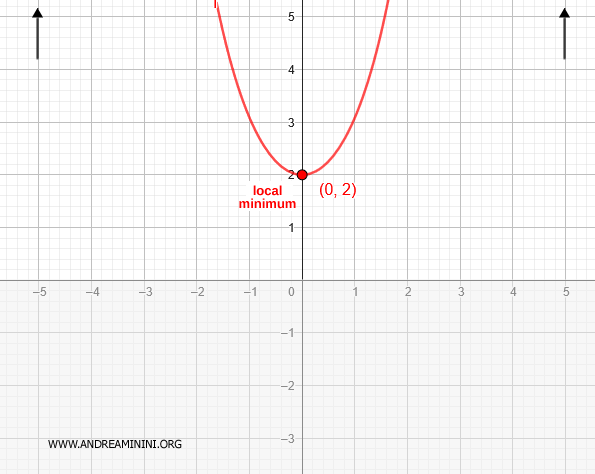
Con ello queda finalizado el análisis.