Ejercicio de análisis de funciones 8

Vamos a estudiar la función exponencial

$$ f(x) = e^{\frac{1}{x}} $$

empleando las técnicas habituales del cálculo diferencial.

Dominio

La función está definida para todos los números reales, salvo en $ x = 0 $:

$$ D_f = \mathbb{R} \setminus \{0\} $$

En $ x = 0 $, el exponente $ \frac{1}{x} $ no existe debido a la división entre cero, lo que convierte este punto en una discontinuidad.

Intersecciones

Como la función no está definida en $ x = 0 $, no tiene intersección con el eje y.

Para verificar si existen intersecciones con el eje x, planteamos la ecuación:

$$ f(x) = e^{\frac{1}{x}} = 0 $$

Aplicamos el logaritmo natural en ambos lados:

$$ \ln\left(e^{\frac{1}{x}}\right) = \ln(0) $$

El miembro izquierdo se reduce a $ \frac{1}{x} $, pero dado que $ \ln(0) $ no está definido, la ecuación carece de solución.

En conclusión, la función no posee intersecciones ni con el eje x ni con el eje y.

Signo

Este aspecto es inmediato: la función exponencial es siempre estrictamente positiva en todo su dominio.

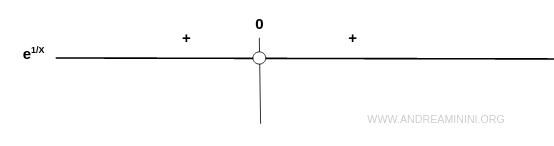
la función es siempre positiva en todo su dominio

Por lo tanto, la gráfica se sitúa por completo en los cuadrantes primero y segundo.

la gráfica ocupa únicamente el primer y segundo cuadrante

Asíntotas horizontales

Para analizar el comportamiento en el infinito, calculamos los límites cuando $ x \to \pm\infty $:

$$ \lim_{x \to \infty} e^{\frac{1}{x}} = 1^+ $$

Nota: cuando $ x \to \infty $, el exponente $ \frac{1}{x} \to 0^+ $, y la función tiende a 1 desde arriba.

$$ \lim_{x \to -\infty} e^{\frac{1}{x}} = 1^- $$

Nota: cuando $ x \to -\infty $, el exponente $ \frac{1}{x} \to 0^- $, y la función se aproxima a 1 desde abajo.

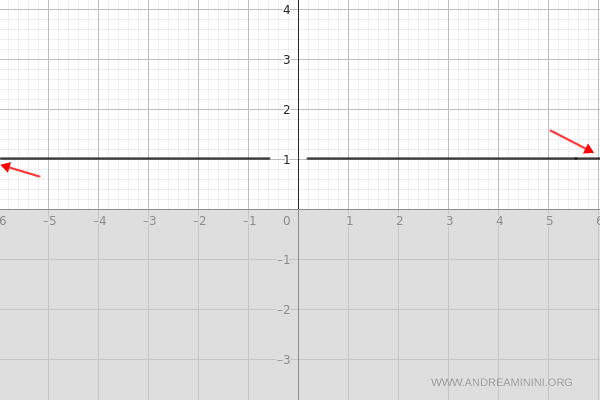
Como ambos límites laterales coinciden en el mismo valor, la función tiene una asíntota horizontal en $ y = 1 $.

asíntota horizontal en y = 1

Asíntotas verticales

Las asíntotas verticales solo pueden darse en los puntos de discontinuidad. En este caso, la función no está definida en $ x = 0 $.

Examinemos su comportamiento en torno a este punto:

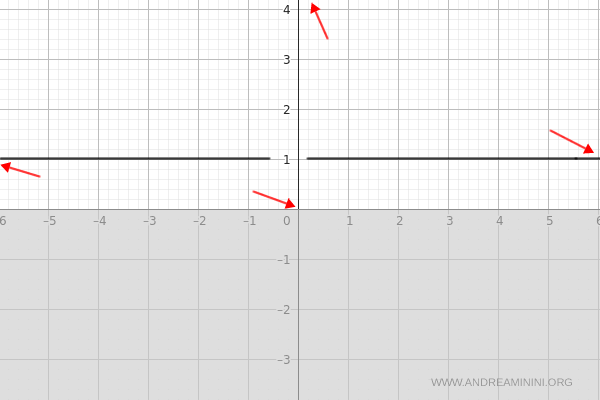
$$ \lim_{x \to 0^+} e^{\frac{1}{x}} = +\infty $$

$$ \lim_{x \to 0^-} e^{\frac{1}{x}} = 0 $$

Como los límites laterales no coinciden, no existe una asíntota vertical en $ x = 0 $.

comportamiento discontinuo en las proximidades de x = 0

Monotonía

Para determinar dónde la función crece o decrece, calculamos la primera derivada:

$$ f'(x) = \frac{d}{dx}\left(e^{\frac{1}{x}}\right) $$

Aplicando la regla de la cadena:

$$ f'(x) = e^{\frac{1}{x}} \cdot \left(-\frac{1}{x^2}\right) = -\frac{e^{\frac{1}{x}}}{x^2} $$

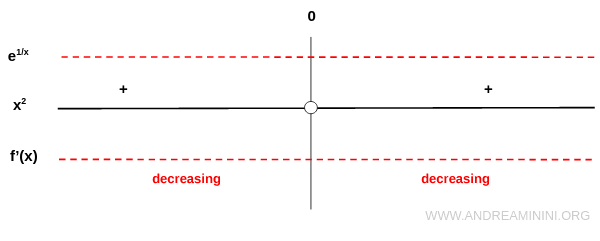
la primera derivada es siempre negativa en todo el dominio

Dado que $ e^{1/x} > 0 $ y $ x^2 > 0 $ para todo $ x \neq 0 $, la derivada resulta negativa en todo el dominio.

Por consiguiente, la función es estrictamente decreciente en todo su dominio.

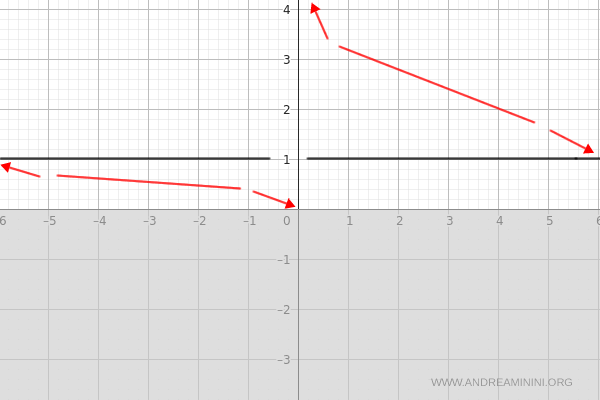
la función decrece de forma continua en todo su dominio

Extremos locales

Como la primera derivada nunca se anula, la función no presenta máximos ni mínimos locales.

Concavidad y puntos de inflexión

Para estudiar la concavidad, calculamos la segunda derivada:

$$ f''(x) = \frac{d}{dx} \left(-\frac{e^{\frac{1}{x}}}{x^2} \right) $$

Aplicando la regla del cociente:

$$ f''(x) = -\frac{ \left( e^{\frac{1}{x}} \cdot \left(-\frac{1}{x^2}\right) \cdot x^2 \right) - \left( e^{\frac{1}{x}} \cdot 2x \right) }{x^4} $$

$$ f''(x) = \frac{ e^{\frac{1}{x}} (1 + 2x) }{x^4} $$

Analizamos ahora el signo de esta expresión:

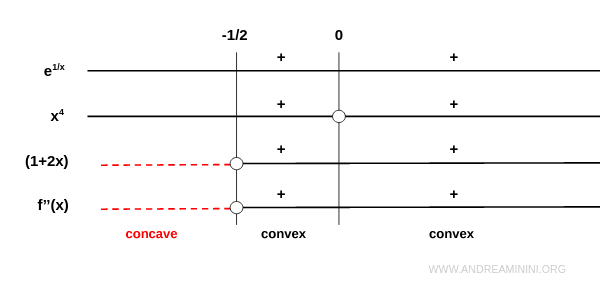
segunda derivada: punto de inflexión en x = -1/2

De aquí se desprenden las siguientes conclusiones:

Cóncava hacia abajo en $ (-\infty, -\frac{1}{2}) $
Cóncava hacia arriba en $ (-\frac{1}{2}, \infty) $

En $ x = -\frac{1}{2} $, la concavidad cambia de signo, por lo que la función tiene un punto de inflexión.

El gráfico completo de la función se muestra a continuación:

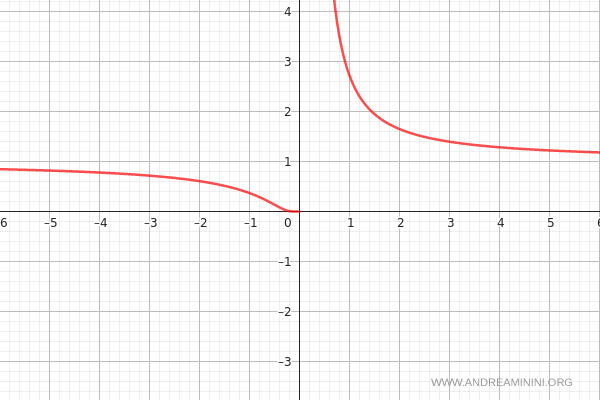
gráfico completo de la función con asíntotas y concavidad destacadas

Y el análisis continúa a partir de aquí.