Ejercicio de análisis de funciones exponenciales 11
En este ejercicio estudiaremos el comportamiento de la función exponencial
$$ f(x) = \frac{x}{e^x} $$
Comencemos determinando su dominio.
Dominio
La función exponencial \( e^x \) nunca se anula para ningún número real. En consecuencia, el cociente \( \frac{x}{e^x} \) está bien definido en toda la recta real:
$$ D_f = ( -\infty , \infty ) $$
Puntos de discontinuidad
Dado que \( e^x \) jamás se hace cero, la función es continua en todo su dominio y no presenta puntos de discontinuidad.
Asíntotas horizontales
Analicemos primero el comportamiento cuando \( x \to +\infty \):
$$ \lim_{x \to \infty} \frac{x}{e^x} = \frac{\infty}{\infty} $$
Se trata de una forma indeterminada. Para evaluarla aplicamos la regla de L’Hôpital:
$$ \lim_{x \to \infty} \frac{1}{e^x} = 0^+ $$
Por lo tanto, la función tiende a cero cuando \( x \to +\infty \):
En cambio, si consideramos el límite cuando \( x \to -\infty \):
$$ \lim_{x \to -\infty} \frac{x}{e^x} = \frac{-\infty}{0^+} = -\infty $$
La función diverge hacia menos infinito en ese extremo.
Asíntotas verticales
Como la función está definida para todo \( x \in \mathbb{R} \), no aparecen asíntotas verticales.
Intersecciones
Para determinar la intersección con el eje y, evaluamos en \( x = 0 \):
$$ f(0) = \frac{0}{e^0} = \frac{0}{1} = 0 $$
La curva pasa, por tanto, por el origen: (0, 0).
Para las intersecciones con el eje x resolvemos:
$$ \frac{x}{e^x} = 0 $$
Multiplicando ambos miembros por \( e^x \):
$$ x = 0 $$
La única intersección con el eje x se encuentra en el origen.
Análisis del signo
Examinemos ahora el signo de la función:
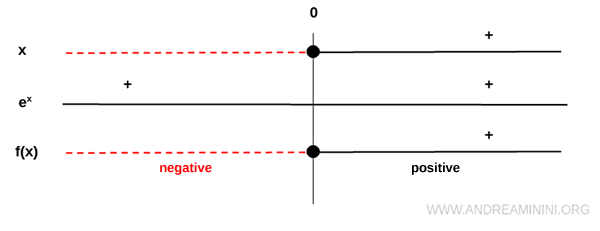
El denominador \( e^x \) es siempre positivo, mientras que el numerador \( x \) es negativo para \( x < 0 \) y positivo para \( x > 0 \).
Por lo tanto, \( f(x) \) es negativa en el semieje izquierdo y positiva en el derecho.
Esto nos permite delimitar con precisión los cuadrantes en los que se sitúa la curva.

Comportamiento creciente y decreciente
Para identificar los intervalos de crecimiento y decrecimiento, calculamos la primera derivada:
$$ f'(x) = D_x\left[ \frac{x}{e^x} \right] = \frac{e^x - x e^x}{(e^x)^2} = \frac{1 - x}{e^x} $$
De manera equivalente, escribiendo \( f(x) = x \cdot e^{-x} \) y aplicando la regla del producto obtenemos: $$ f'(x) = D_x[x] \cdot e^{-x} + x \cdot D_x[e^{-x}] = e^{-x} - x e^{-x} = e^{-x}(1 - x) = \frac{1 - x}{e^x} $$
Analizamos el signo de \( f'(x) \):
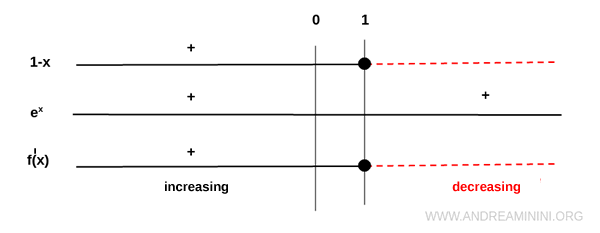
La derivada es positiva para \( x < 1 \) y negativa para \( x > 1 \). En consecuencia, la función crece en el intervalo \( (-\infty, 1) \) y decrece en \( (1, \infty) \).
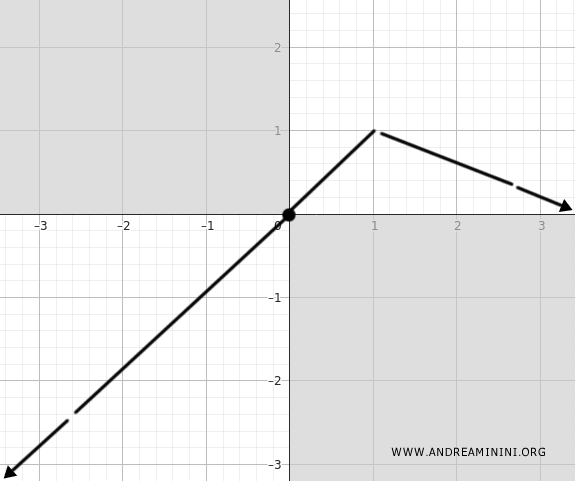
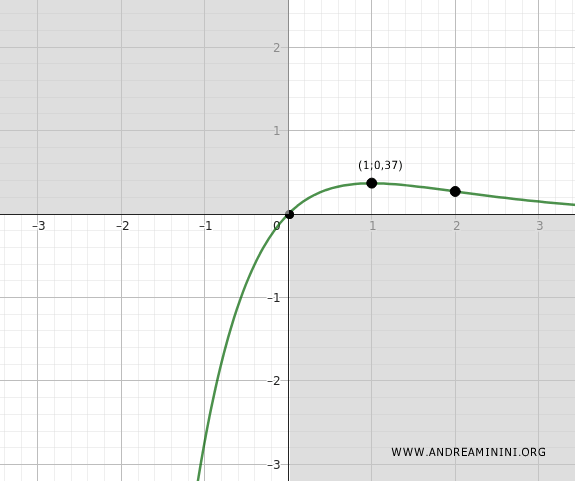
En \( x = 1 \), la derivada se anula y cambia de signo de positiva a negativa. Por ello, la función alcanza en este punto un máximo local.
Calculamos su valor:
$$ f(1) = \frac{1}{e} \approx 0.37 $$
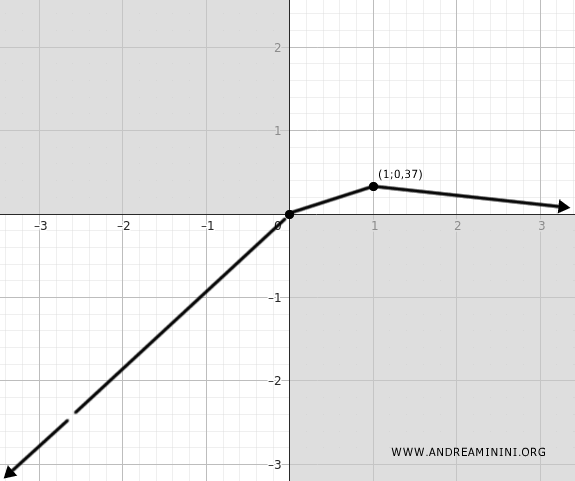
El máximo local se localiza en el punto (1, 0.37).
Concavidad, convexidad y puntos de inflexión
Para estudiar la curvatura y determinar la presencia de posibles puntos de inflexión, calculamos la segunda derivada:
$$ f''(x) = D_x\left[ \frac{1 - x}{e^x} \right] = \frac{-e^x - (1 - x) e^x}{(e^x)^2} $$
$$ = \frac{-2e^x + x e^x}{(e^x)^2} = \frac{e^x(x - 2)}{(e^x)^2} = \frac{x - 2}{e^x} $$
Estudiamos ahora el signo de la segunda derivada:
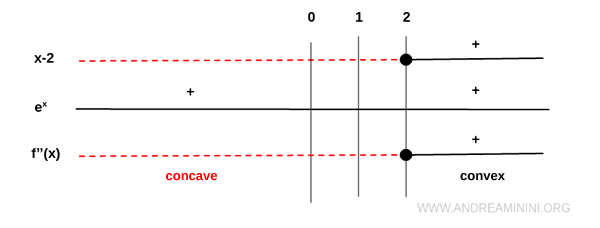
La segunda derivada es negativa para \( x < 2 \), lo que indica concavidad hacia abajo, y positiva para \( x > 2 \), lo que indica convexidad.
En \( x = 2 \), se cumple \( f''(x) = 0 \) y el signo cambia, lo que confirma la existencia de un punto de inflexión.
Para determinar su ordenada, evaluamos en \( x = 2 \):
$$ f(2) = \frac{2}{e^2} \approx 0.27 $$
El punto de inflexión se encuentra en (2, 0.27).
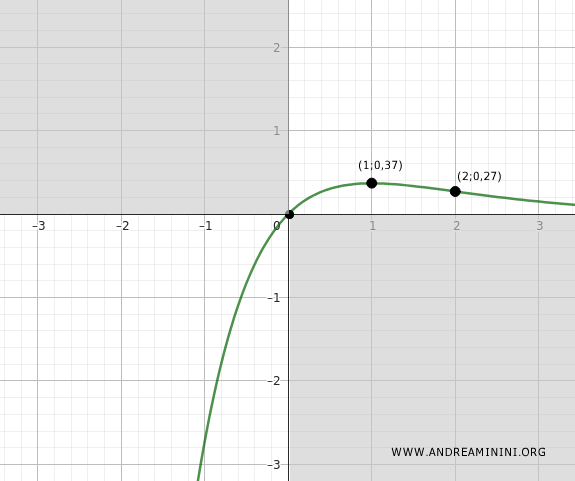
Con este estudio hemos descrito de manera completa la función: conocemos su dominio, su signo, sus intersecciones, la ausencia de asíntotas verticales, la existencia de una asíntota horizontal en \( y = 0 \), el máximo local en \( (1, \tfrac{1}{e}) \) y el punto de inflexión en \( (2, \tfrac{2}{e^2}) \). A partir de estos resultados, la representación gráfica queda perfectamente determinada.