Ejercicio de Análisis de Funciones Racionales 5

Estudiaremos ahora la gráfica de la siguiente función racional:

$$ f(x) = \frac{5x-1}{x^2-3x+2} $$

Para ello aplicaremos, de manera sistemática, las técnicas fundamentales del cálculo.

Dominio

El primer paso es determinar el dominio de la función.

Está definida para todos los números reales, salvo en los valores que anulan el denominador.

El denominador $ x^2 - 3x + 2 $ se factoriza de forma inmediata, y sus raíces son:

$$ x = \frac{3 \pm \sqrt{9 - 8}}{2} = \frac{3 \pm 1}{2} $$

$$ x = 1 \quad \text{y} \quad x = 2 $$

Por tanto, el dominio queda descrito como:

$$ D_f = (-\infty, 1) \cup (1, 2) \cup (2, \infty) $$

La función no está definida en los puntos $ x = 1 $ y $ x = 2 $.

Intersecciones

Para calcular la intersección con el eje y evaluamos en $ x = 0 $:

$$ f(0) = \frac{-1}{2} $$

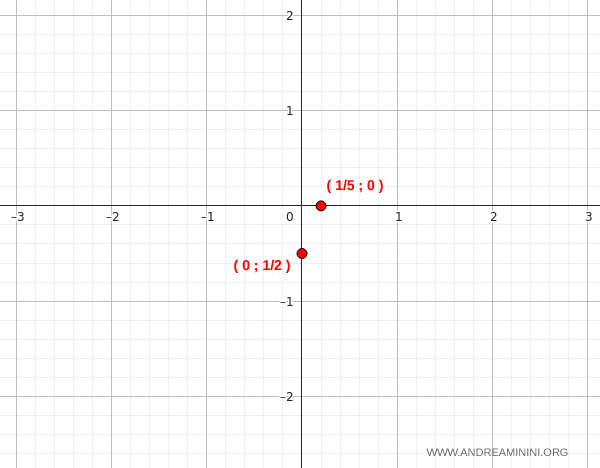
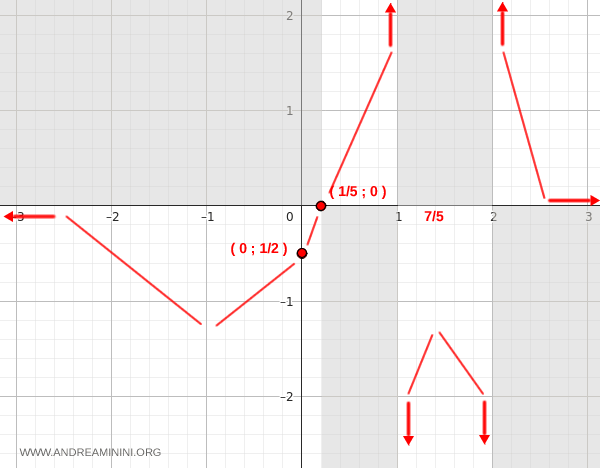
La gráfica pasa por el punto (0, -1/2).

Para la intersección con el eje x resolvemos la ecuación $ f(x) = 0 $:

$$ 5x - 1 = 0 \quad \Rightarrow \quad x = \tfrac{1}{5} $$

De este modo, la gráfica corta el eje x en el punto (1/5, 0).

intersecciones de la función con los ejes

Análisis de signos

Examinemos ahora el signo de la función.

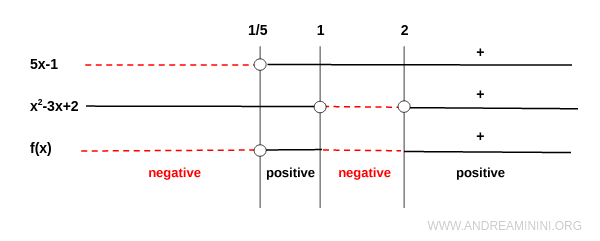
análisis de signos de la función

Estudiamos por separado numerador y denominador:

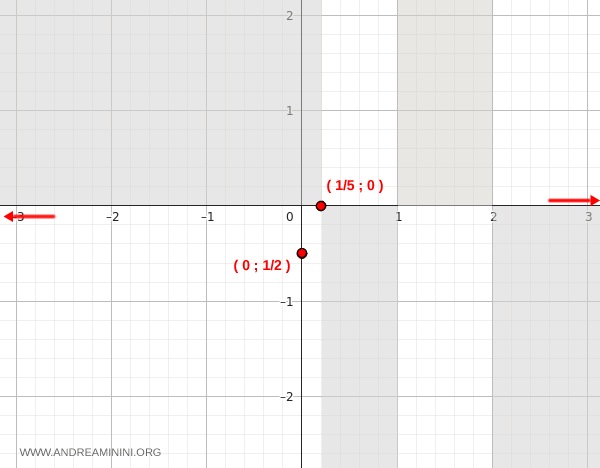
El numerador $ 5x - 1 $ es positivo si $ x > \tfrac{1}{5} $, nulo en $ x = \tfrac{1}{5} $ y negativo si $ x < \tfrac{1}{5} $.
El denominador $ x^2 - 3x + 2 $ corresponde a una parábola con apertura hacia arriba, cuyas raíces son $ x = 1 $ y $ x = 2 $. Es positivo en $ (-\infty, 1) \cup (2, \infty) $ y negativo en $ (1, 2) $.

Combinando ambas condiciones concluimos que:

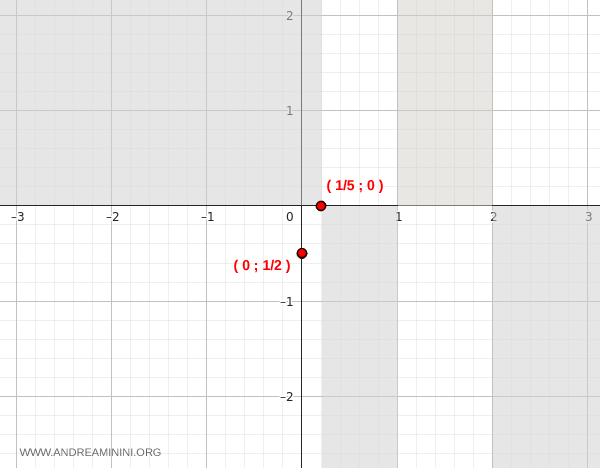
La función es negativa en $ (-\infty, \tfrac{1}{5}) $ y en $ (1, 2) $.
La función es positiva en $ (\tfrac{1}{5}, 1) $ y en $ (2, \infty) $.

zonas de validez de la función en el plano cartesiano

Asíntotas

Asíntota horizontal

Examinamos ahora el comportamiento de la función cuando $ x \to \pm\infty $:

$$ \lim_{x \to \infty} \frac{5x - 1}{x^2 - 3x + 2} = \frac{\infty}{\infty} $$

Se trata de una forma indeterminada. Aplicamos la regla de L’Hôpital:

$$ \lim_{x \to \infty} \frac{5}{2x - 3} = 0^+ $$

Cuando $ x \to \infty $, la función se aproxima a 0 por valores positivos.

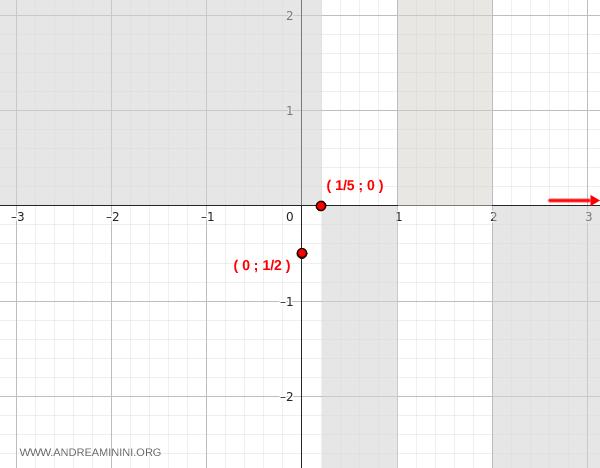
la función tiende a cero desde arriba al tender a infinito

De forma análoga, para $ x \to -\infty $:

$$ \lim_{x \to -\infty} \frac{5}{2x - 3} = 0^- $$

Cuando $ x \to -\infty $, la función se aproxima a 0 por valores negativos.

En consecuencia, la función presenta una asíntota horizontal en el eje x: $ y = 0 $.

la función tiende a cero desde abajo al tender a menos infinito

Asíntotas verticales

Las asíntotas verticales aparecen en aquellos valores de $ x $ donde la función diverge cuando el denominador se anula.

Hemos identificado como candidatos los puntos $ x = 1 $ y $ x = 2 $.

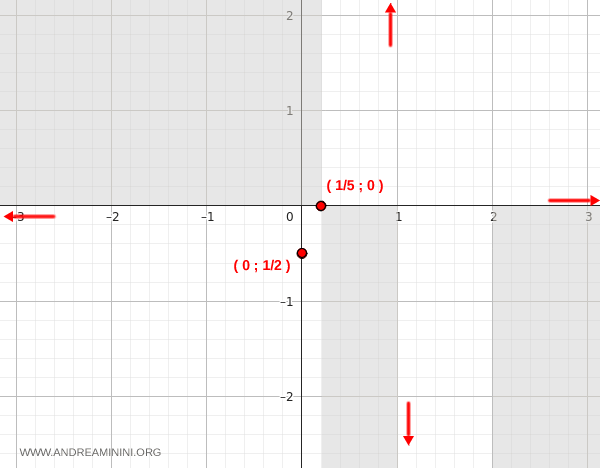
Analicemos primero el comportamiento en torno a $ x = 1 $:

$$ \lim_{x \to 1^+} \frac{5x - 1}{x^2 - 3x + 2} = \frac{4}{0^+} = -\infty $$

$$ \lim_{x \to 1^-} \frac{5x - 1}{x^2 - 3x + 2} = \frac{4}{0^-} = +\infty $$

Los límites laterales divergen con signos opuestos, pero ambos son infinitos. Por lo tanto, en $ x = 1 $ existe una asíntota vertical.

asíntota vertical en x = 1 con límites laterales de signo opuesto

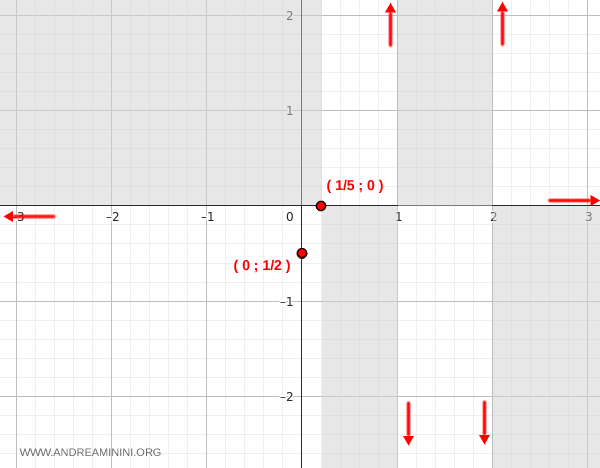
Procedamos ahora con $ x = 2 $:

$$ \lim_{x \to 2^+} \frac{5x - 1}{x^2 - 3x + 2} = \frac{9}{0^+} = +\infty $$

$$ \lim_{x \to 2^-} \frac{5x - 1}{x^2 - 3x + 2} = \frac{9}{0^-} = -\infty $$

También en este caso los límites laterales divergen con signos opuestos. Por lo tanto, en $ x = 2 $ existe una asíntota vertical.

asíntota vertical en x = 2 con límites laterales de signo opuesto

Monotonía

Para determinar los intervalos de crecimiento y decrecimiento, calculamos la primera derivada:

$$ f'(x) = \frac{ -5x^2 + 2x + 7 }{(x^2 - 3x + 2)^2} $$

El denominador es siempre positivo (excepto en los puntos de discontinuidad), de manera que el signo de $ f'(x) $ depende únicamente del numerador.

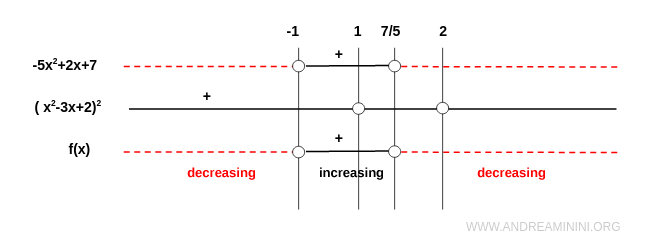
tabla de signos de la primera derivada

Nota. El numerador $ -5x^2 + 2x + 7 $ describe una parábola abierta hacia abajo. Sus raíces son:

$$ x = \frac{-2 \pm \sqrt{2^2 - 4(-5)(7)}}{2(-5)} = \frac{-2 \pm \sqrt{144}}{-10} = \frac{-2 \pm 12}{-10} $$

$$ x = -1 \quad \text{y} \quad x = \tfrac{7}{5} $$

En consecuencia, la función es decreciente en $ (-\infty, -1) \cup \left(\tfrac{7}{5}, \infty\right) $, y creciente en $ (-1, \tfrac{7}{5}) $.

intervalos de crecimiento y decrecimiento

Los puntos críticos, donde $ f'(x) = 0 $, son:

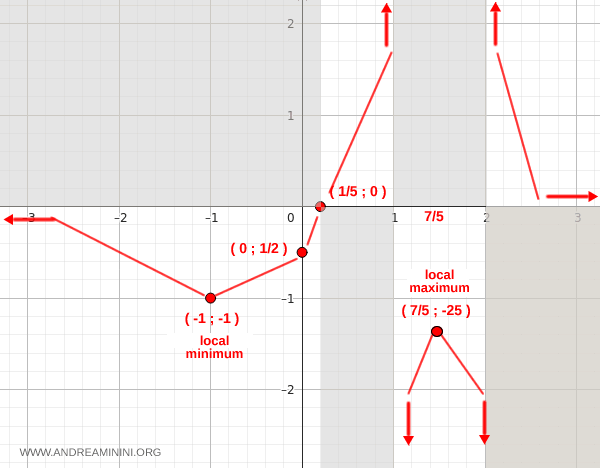
En $ x = -1 $, la derivada cambia de negativa a positiva, por lo que se trata de un mínimo local. $$ f(-1) = \frac{5(-1) - 1}{(-1)^2 - 3(-1) + 2} = \frac{-6}{6} = -1 $$ El mínimo local se ubica en (-1, -1).
En $ x = \tfrac{7}{5} $, la derivada pasa de positiva a negativa, lo que indica un máximo local. $$ f\!\left(\tfrac{7}{5}\right) = \frac{6}{\tfrac{49}{25} - \tfrac{21}{5} + 2} = \frac{6}{-\tfrac{6}{25}} = -25 $$ Así, el máximo local se encuentra en $\big(\tfrac{7}{5}, -25\big)$.

extremos locales de la función

Concavidad e inflexión

Para analizar la curvatura de la función calculamos la segunda derivada:

$$ f''(x) = \frac{ 10x^3 - 6x^2 - 42x + 46 }{(x^2 - 3x + 2)^3} $$

El numerador es un polinomio cúbico que cambia de signo en un punto $ \beta < -2 $. Para valores $ x > -2 $, el numerador es positivo.

signo de la segunda derivada

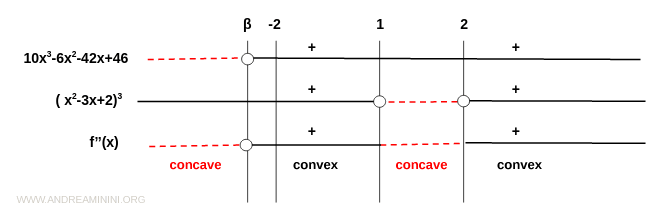
De ello se deduce:

La función es cóncava hacia abajo en $ (-\infty, \beta) $
Cóncava hacia arriba en $ (\beta, 1) $
Cóncava hacia abajo en $ (1, 2) $
Cóncava hacia arriba en $ (2, \infty) $

El punto $ x = \beta $ corresponde a un punto de inflexión, ya que en él la concavidad cambia de signo.

La gráfica completa de la función es la siguiente:

gráfica final de la función racional