Function Analysis Exercise 9

We are asked to analyze the function

$$ f(x) = \sqrt{x^2 - 16} $$

using the standard techniques of differential calculus.

Domain

The square root is defined only when its argument is non-negative:

$$ x^2 - 16 \geq 0 $$

$$ x^2 \geq 16 $$

Taking square roots and considering both signs gives:

$$ |x| \geq 4 $$

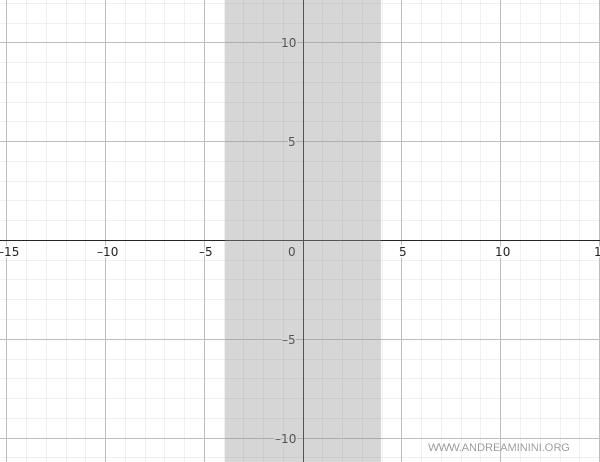
Hence, the domain is:

$$ D_f = (-\infty, -4] \cup [4, \infty) $$

On the graph, the interval $ (-4, 4) $ must be excluded, as the function is undefined there.

function undefined in the interval (-4, 4)

Intercepts

There is no y-intercept since $ f(0) $ is undefined.

To find the x-intercepts, we solve:

$$ \sqrt{x^2 - 16} = 0 $$

Squaring both sides yields:

$$ x^2 - 16 = 0 \quad \Rightarrow \quad x^2 = 16 $$

Thus:

$$ x = \pm 4 $$

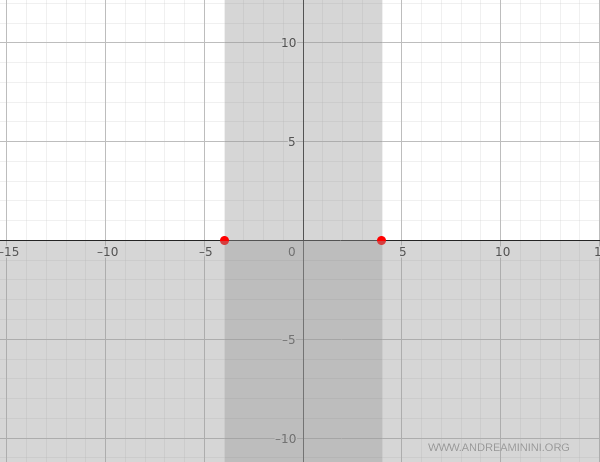
The function intersects the x-axis at the points $ (-4, 0) $ and $ (4, 0) $.

Sign Analysis

Being a square root, the function takes only non-negative values. It is strictly positive everywhere in its domain, except at the boundary points $ x = \pm 4 $, where it equals zero.

sign of the function: non-negative values only

Therefore, the graph lies entirely on or above the x-axis, and the lower half-plane can be disregarded.

function values are always above or on the x-axis

Asymptotic Behavior

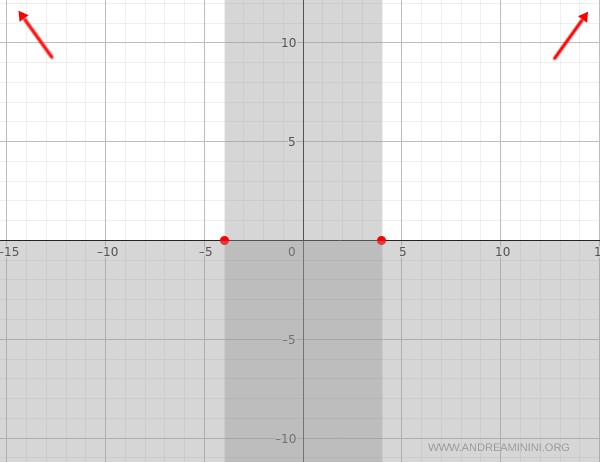
Consider the end behavior as $ x \to \pm\infty $:

$$ \lim_{x \to \infty} \sqrt{x^2 - 16} = +\infty, \quad \lim_{x \to -\infty} \sqrt{x^2 - 16} = +\infty $$

In both directions, the function diverges to infinity.

end behavior: function diverges as x approaches ±infinity

Monotonicity

The first derivative is:

$$ f'(x) = \frac{d}{dx}\left(\sqrt{x^2 - 16}\right) = \frac{x}{\sqrt{x^2 - 16}} $$

Its sign depends directly on the numerator:

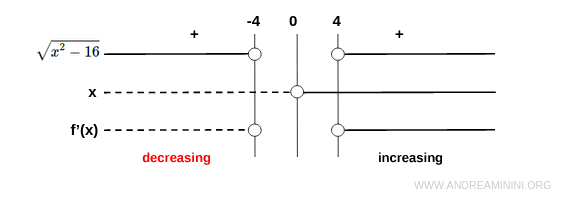
sign analysis of the first derivative

For $ x < -4 $, $ f'(x) < 0 $: the function decreases. For $ x > 4 $, $ f'(x) > 0 $: the function increases.

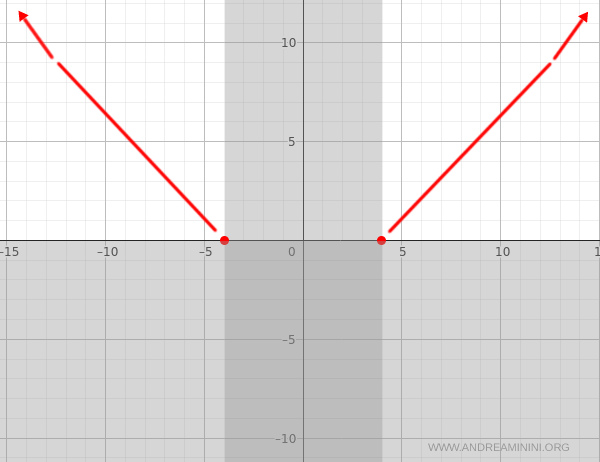
function is decreasing for x < -4 and increasing for x > 4

Local Extrema

The derivative never vanishes within the domain, so there are no local maxima or minima in the usual sense.

Concavity and Inflection Points

Now let us compute the second derivative:

$$ f''(x) = \frac{d}{dx}\left(\frac{x}{\sqrt{x^2 - 16}}\right) $$

After simplification, we obtain:

$$ f''(x) = \frac{-16}{(x^2 - 16)\sqrt{x^2 - 16}} $$

This is always negative throughout the domain.

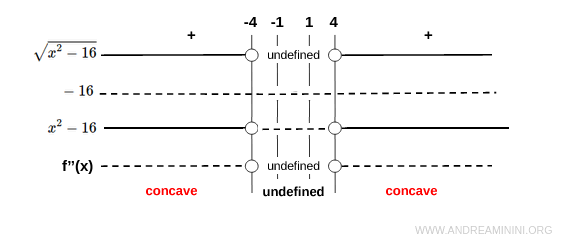
second derivative is always negative: graph is concave down

Therefore, $ f(x) $ is concave downward everywhere it is defined: on both $ (-\infty, -4] $ and $ [4, \infty) $.

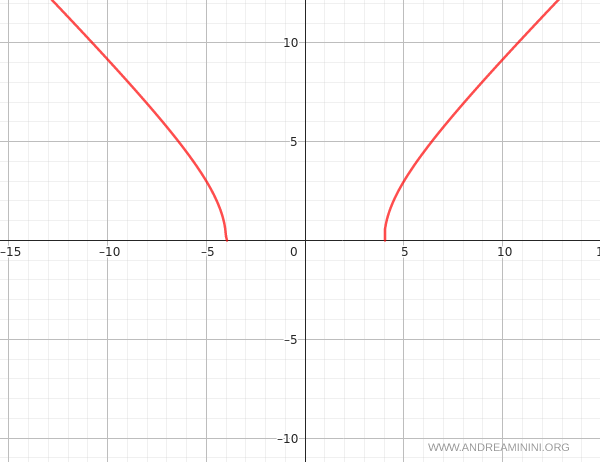
final plot of the function graph

With this, the essential features of the graph are fully determined.