Teorema de la base en la topología inducida por una métrica

En un espacio métrico $(X, d)$, la colección de bolas abiertas $$ \mathcal{B} = \{B_d(x, \varepsilon) \mid x \in X, \varepsilon > 0\} $$ constituye una base para una topología sobre $X$.

Una familia de conjuntos abiertos $\mathcal{B}$ es una base para una topología si todo conjunto abierto puede escribirse como una unión de elementos de dicha familia.

En particular, se dice que una colección $\mathcal{B}$ es una base si cumple las siguientes dos condiciones:

Para todo punto $x \in X$, existe al menos un conjunto $B \in \mathcal{B}$ tal que $x \in B$. (Recubrimiento)
Si $x \in B_1 \cap B_2$, con $B_1, B_2 \in \mathcal{B}$, entonces existe un conjunto $B_3 \in \mathcal{B}$ tal que $x \in B_3 \subseteq B_1 \cap B_2$. (Compatibilidad con la intersección)

El teorema establece que la colección de todas las bolas abiertas $B_d(x, \varepsilon)$ cumple ambas condiciones, por lo que define una topología sobre $X$.

Una bola abierta es el conjunto de todos los puntos $y \in X$ cuya distancia a $x$ es menor que un cierto $\varepsilon > 0$: $$ B_d(x, \varepsilon) = \{y \in X \mid d(x, y) < \varepsilon\}. $$

En otras palabras, este teorema demuestra que la estructura topológica de un espacio métrico puede describirse por completo a partir de las bolas abiertas.

Un ejemplo
Demostración

Un ejemplo

Consideremos un conjunto abierto $A$ en el plano $\mathbb{R}^2$, definido del siguiente modo:

$$ A = \{(x_1, x_2) \in \mathbb{R}^2 \mid 1 < x_1^2 + x_2^2 < 4 \} $$

Geométricamente, este conjunto representa una corona circular en el plano, delimitada por dos circunferencias de radios 1 y 2.

Se trata de un conjunto abierto, ya que no incluye los puntos de la frontera.

corona circular abierta en el plano

¿Cómo se puede expresar $A$ como una unión de bolas abiertas?

De acuerdo con el teorema de la base, $A$ puede describirse como una unión de bolas abiertas.

Para ello, basta con tomar múltiples bolas abiertas centradas en puntos del interior de la corona, cada una con un radio lo bastante pequeño como para quedar contenida íntegramente en $A$.

Por ejemplo, consideremos la bola abierta centrada en el punto $p_1 = (1.5, 0)$ con radio $\varepsilon_1 = 0.3$:

$$ B1_d((1.5, 0), 0.3) = \{(x_1, x_2) \in \mathbb{R}^2 \mid d((1.5, 0), (x_1, x_2)) < 0.3\} $$

Esta bola está completamente contenida en la corona $A$.

bola contenida en la corona

Ahora consideremos la bola centrada en $p_2 = (-1.5, 0)$ con radio $\varepsilon_2 = 0.4$:

$$ B2_d((-1.5, 0), 0.4) = \{(x_1, x_2) \in \mathbb{R}^2 \mid d((-1.5, 0), (x_1, x_2)) < 0.4\} $$

Esta bola también se encuentra completamente dentro del conjunto $A$.

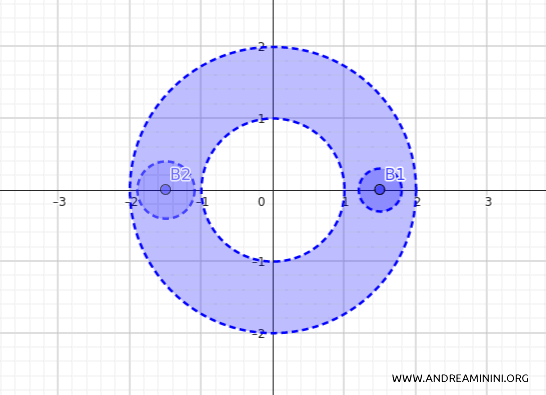
segunda bola dentro del conjunto

Repitiendo este procedimiento, podemos construir muchas otras bolas abiertas centradas en distintos puntos de la corona, todas con radios suficientemente pequeños para mantenerse dentro de $A$.

La idea clave es que podemos cubrir el conjunto $A$ por completo mediante la unión de estas bolas abiertas, sin dejar espacios sin cubrir.

Formalmente, se puede escribir:

$$ A = \bigcup_{i} B_d(x_i, \varepsilon_i) $$

Donde $x_i$ son los centros y $\varepsilon_i$ los radios de las distintas bolas abiertas contenidas en $A$.

Este ejemplo muestra cómo cualquier conjunto abierto (como la corona $A$) en $\mathbb{R}^2$ puede expresarse como una unión de bolas abiertas.

En definitiva, las bolas abiertas actúan como los “bloques básicos” que permiten construir todos los conjuntos abiertos en una topología inducida por métrica.

Demostración

Queremos demostrar que la colección de bolas abiertas en un espacio métrico $(X, d)$ constituye una base para una topología sobre $X$.

Para ello, verificamos que se cumplen las condiciones necesarias:

1] La primera condición exige que todo punto del espacio pertenezca a alguna bola abierta

Esto es inmediato: para cualquier $x \in X$, la bola abierta $B_d(x, \varepsilon)$ centrada en $x$, con $\varepsilon > 0$, contiene a $x$.

Así, toda bola abierta contiene a su centro, lo que garantiza que cada punto está contenido al menos en una bola.

2] La segunda condición establece que, si $x$ pertenece a la intersección de dos bolas abiertas $B_1$ y $B_2$, debe existir una bola $B_3$, también abierta y centrada en $x$, que esté completamente contenida en la intersección $B_1 \cap B_2$.

Esta propiedad es esencial, ya que permite “refinar” las bolas abiertas sin salirnos del entorno común de $x$.

Sean $B_1 = B_d(x_1, \varepsilon_1)$ y $B_2 = B_d(x_2, \varepsilon_2)$, y supongamos que $x \in B_1 \cap B_2$.

Como $x$ pertenece tanto a $B_1$ como a $B_2$, podemos encontrar radios $\delta_1$ y $\delta_2$ tales que:

Existe una bola $B_d(x, \delta_1)$ contenida en $B_1$.
Existe una bola $B_d(x, \delta_2)$ contenida en $B_2$.

Entonces, si tomamos $\delta = \min\{\delta_1, \delta_2\}$, la bola $B_d(x, \delta)$ estará contenida tanto en $B_1$ como en $B_2$, y por tanto en su intersección.

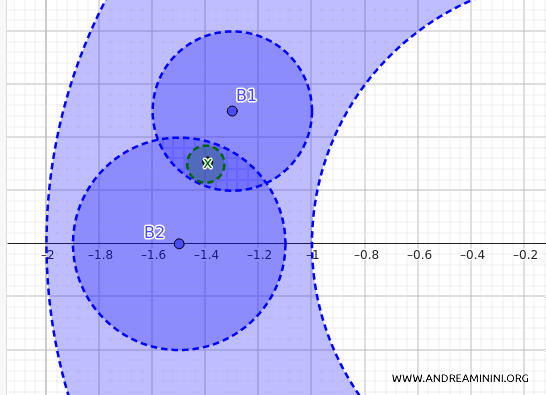
intersección refinada de bolas abiertas

La segunda condición también queda demostrada.

En conclusión, hemos probado que la colección de bolas abiertas satisface ambas condiciones necesarias para constituir una base.

Por tanto, dicha colección define una topología sobre $X$, conocida como la topología inducida por la métrica.

Y así se concluye.