Ensemble borné en topologie métrique
Dans un espace métrique \((X, d)\), où \(d\) est la fonction qui mesure la distance entre les points, un sous-ensemble \(A \subseteq X\) est dit borné s’il existe un réel strictement positif \(\mu > 0\) tel que, pour tout couple de points \(x, y \in A\), on ait \(d(x, y) \leq \mu\).
Autrement dit, les points de \(A\) sont tous contenus dans une "zone" dont le diamètre ne dépasse pas \(\mu\).
Si l’ensemble \(X\) lui-même est borné pour la métrique \(d\), on dit alors que \(d\) est une métrique bornée.
Cela signifie que la distance entre n’importe quels deux points de \(X\) est toujours inférieure ou égale à une certaine constante \(\mu\).
Remarque : Si la métrique \(d\) est bornée, tout sous-ensemble de \(X\) l’est nécessairement aussi, puisque ses distances internes ne peuvent excéder celles de l’ensemble global.
Un exemple concret
Considérons le plan cartésien \(\mathbb{R}^2\) muni de la distance euclidienne classique.
La distance entre deux points \((x_1, y_1)\) et \((x_2, y_2)\) est donnée par :
$$ d((x_1, y_1), (x_2, y_2)) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
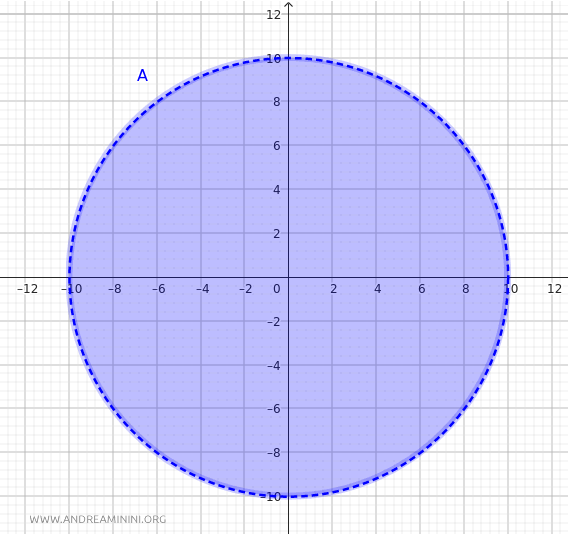
Soit maintenant le sous-ensemble \(A \subseteq \mathbb{R}^2\) constitué de tous les points \((x, y)\) situés à l’intérieur (ou sur le bord) d’un disque de rayon \(10\) centré à l’origine :
$$ A = \{(x, y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 10^2\} $$
Ce sous-ensemble est borné s’il existe une constante \(\mu > 0\) telle que, pour tout couple \((x_1, y_1), (x_2, y_2) \in A\), on ait \(d((x_1, y_1), (x_2, y_2)) \leq \mu\).
La distance maximale entre deux points de \(A\) est atteinte lorsque ceux-ci se trouvent aux extrémités d’un diamètre (par exemple, \((10, 0)\) et \((-10, 0)\)).
Dans ce cas :
$$ d((10, 0), (-10, 0)) = \sqrt{((-10) - 10)^2 + (0 - 0)^2} = \sqrt{400} = 20 $$
Ainsi, quelle que soit la paire de points choisie dans le disque, leur distance est toujours inférieure ou égale à \(20\).
On en conclut que l’ensemble \(A\) est borné, avec \(\mu = 20\), puisque tous ses éléments sont contenus dans une région de diamètre fini.
Le caractère borné d’une métrique n’affecte pas la topologie
Il est essentiel de comprendre que le fait qu’une métrique soit bornée ou non n’a aucune incidence sur la topologie qu’elle induit, c’est-à-dire sur la structure des ensembles ouverts ou fermés.
Qu’est-ce que la topologie ? La topologie est le cadre conceptuel qui permet de définir rigoureusement les notions d’ensembles ouverts et fermés. Elle dépend de la manière dont l’espace est structuré, et non des valeurs numériques prises par la métrique.
Par conséquent, même lorsqu’une métrique n’est pas bornée, il est toujours possible d’en construire une autre, équivalente au sens topologique, qui soit bornée et induise exactement la même topologie.
En d’autres termes, le caractère borné ou non de la métrique n’affecte en rien les propriétés topologiques de l’espace.
Exemple
Pour obtenir une métrique bornée à partir d’une métrique non bornée, on peut utiliser une transformation qui "compresse" les grandes distances tout en préservant la topologie.
Un procédé fréquent consiste à appliquer la transformation suivante :
$$ d'(x, y) = \frac{d(x, y)}{1 + d(x, y)} $$
Quel est l’effet de cette transformation ?
Lorsque \(d(x, y)\) est petite, on a \(d'(x, y) \approx d(x, y)\).
Par exemple, si \(d(x, y) = 1\), alors :
$$ d'(x, y) = \frac{1}{1 + 1} = 0{,}5 $$
En revanche, si \(d(x, y)\) est très grande (tend vers l’infini), alors \(d'(x, y)\) tend vers \(1\).
Ainsi, toutes les distances sont ramenées dans l’intervalle \([0, 1)\), sans modifier la structure topologique de l’espace.
Considérons à présent un exemple concret : l’espace métrique \((X, d)\) muni de la distance usuelle \(d(x, y) = |x - y|\), qui est non bornée.
Après transformation, on obtient :
$$ d'(x, y) = \frac{|x - y|}{1 + |x - y|} $$
Si \(x = 1\) et \(y = 2\), alors :
$$ d'(1, 2) = \frac{1}{1 + 1} = 0{,}5 $$
Et si \(x = 1\) et \(y = 1000\), alors :
$$ d'(1, 1000) = \frac{999}{1 + 999} = 0{,}999 $$
Dans tous les cas, les distances restent strictement inférieures à \(1\), tout en conservant la même topologie que celle induite par la métrique initiale.
Les ensembles ouverts (et fermés) définis par \(d\) et par \(d'\) coïncident donc exactement.
Et ainsi de suite...