Exercices résolus sur les anneaux
Ce module rassemble une série d’exemples entièrement résolus qui permettent de comprendre, pas à pas, comment vérifier si une structure munie de deux opérations forme réellement un anneau. Chaque exercice développe les points essentiels et montre comment appliquer directement les définitions.
Exercice 1
Nous étudions ici l’ensemble des entiers modulo 5 $$ \mathbb{Z}_5 = \{ 0, 1, 2, 3, 4 \} $$ muni de l’addition et de la multiplication modulo 5. L’objectif est de déterminer si cette structure constitue un anneau:
$$ (\mathbb{Z}_5 , +_5, \cdot_5) $$
Comme l’ensemble est fini, commençons par observer ses tables d’opération. Voici la table d’addition:
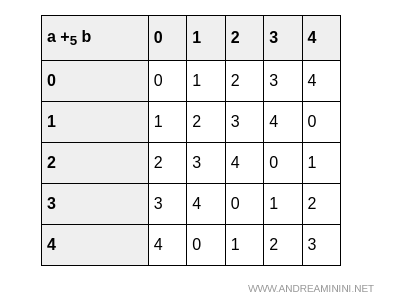
Et sa table de multiplication:
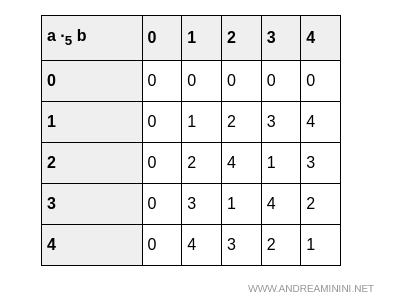
Les opérations sont toutes deux fermées dans l’ensemble, ce qui constitue le premier critère pour avoir un anneau.
Analyse de l’addition ($+_5$)
Les propriétés exigées sont bien présentes: l’addition est commutative, associative, admet un élément neutre (0) et chaque élément possède un inverse additif. Par exemple, $1$ et $4$ s’annulent, tout comme $2$ et $3$.
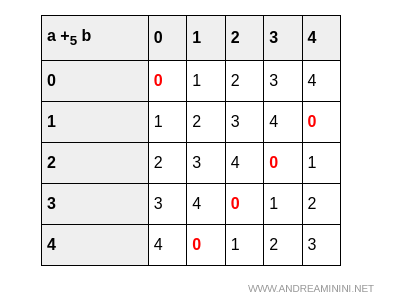
La structure additive répond donc pleinement aux exigences définies dans la théorie des anneaux.
Note: $(\mathbb{Z}_5, +)$ forme un groupe abélien, ce qui est indispensable pour que l’ensemble puisse être muni d’une structure d’anneau.
Analyse de la multiplication ($\cdot_5$)
La multiplication est associative et distributive par rapport à l’addition, ce qui complète la vérification des axiomes.
Conclusion
Les deux opérations remplissant toutes les conditions, nous concluons que:
$(\mathbb{Z}_5, +, \cdot)$ est un anneau.
Exercice 2
Nous examinons maintenant la fonction $$ f(x) = |x| $$ et nous nous demandons si elle définit un homomorphisme d’anneaux de $(\mathbb{Z}, +, \cdot)$ vers $(\mathbb{Z}', +, \cdot)$.
La première condition à vérifier est la préservation du produit:
$$ f(a \cdot b) = f(a) \cdot f(b) $$
Cette égalité est toujours vraie, car la valeur absolue respecte le produit.
La deuxième condition concerne l’addition:
$$ f(a + b) = f(a) + f(b) $$
Cette fois, l’égalité échoue dès que les signes sont opposés. Par exemple:
$$ |2 + (-3)| = 1 \quad \ne \quad |2| + |-3| = 5 $$
La fonction ne préserve donc pas l’addition et ne peut être un homomorphisme d’anneaux.
Conclusion: la fonction $f(x) = |x|$ n’est pas un homomorphisme d’anneaux.
Exercice 3
Nous étudions maintenant l’ensemble des entiers modulo 6 $$ \mathbb{Z}_6 = \{ 0, 1, 2, 3, 4, 5 \} $$ muni de ses opérations modulo 6, afin de déterminer s’il constitue un anneau.
Voici la table d’addition:
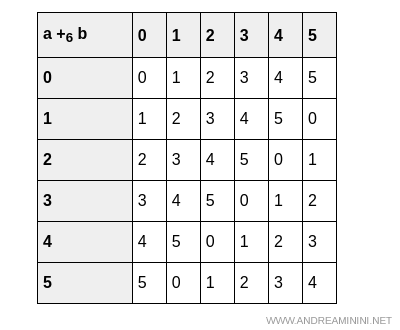
Et la table de multiplication:
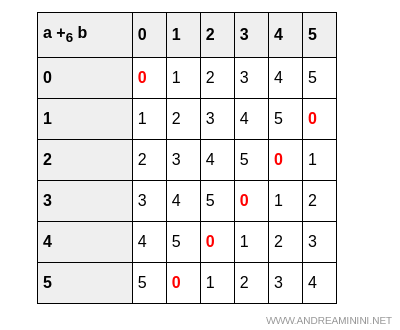
Analyse de l’addition ($+_6$)
L’addition modulo 6 est commutative et associative, possède un neutre (0) et chaque élément possède un inverse additif. Par exemple, $1$ s’annule avec $5$, $2$ avec $4$ et $3$ avec lui-même.
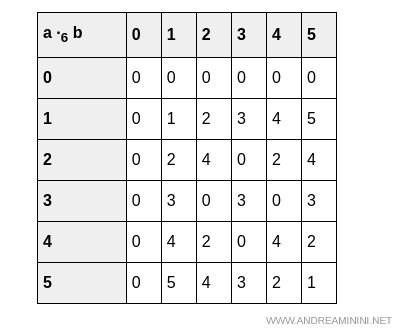
Analyse de la multiplication ($\cdot_6$)
La multiplication satisfait les axiomes requis: elle est associative et distributive par rapport à l’addition.
Conclusion
Les opérations répondant toutes aux critères, on obtient bien que:
$(\mathbb{Z}_6, +, \cdot)$ est un anneau.
Exercice 4
Nous analysons maintenant la fonction $$ f(x) = 3x $$ afin de déterminer si elle définit un homomorphisme d’anneaux de $(\mathbb{Z}_6, +, \cdot)$ dans lui-même, les opérations étant prises modulo 6.
Pour rappel, voici les deux tables d’opération de $\mathbb{Z}_6$:


Préservation de l’addition
$$ f(a + b) = 3(a + b) = 3a + 3b = f(a) + f(b) $$
La fonction respecte donc l’addition modulo 6.
Préservation de la multiplication
$$ f(a \cdot b) = 3(a \cdot b) $$
$$ f(a) \cdot f(b) = (3a) \cdot (3b) $$
L’égalité est vérifiée dans $\mathbb{Z}_6$, car les deux expressions donnent les mêmes résultats modulo 6.
Vérification explicite
Les tableaux suivants montrent que les deux opérations sont effectivement préservées, que l’on calcule $3(a + b)$ ou $3a + 3b$:
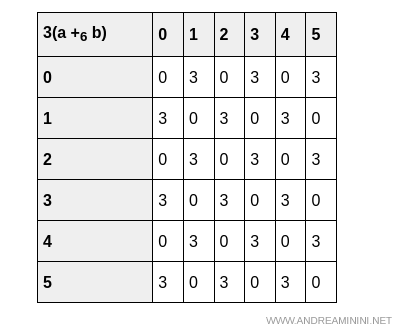
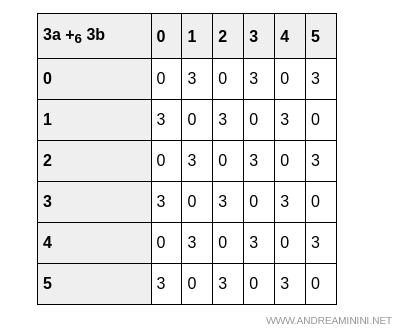
Et de même pour le produit:
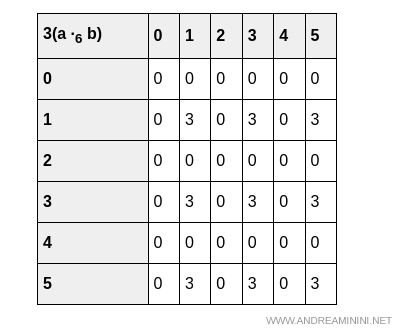
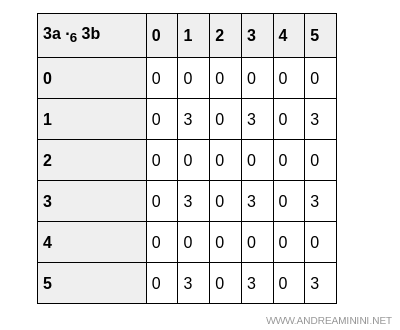
Conclusion
La fonction $$ f(x) = 3x $$ préserve à la fois l’addition et la multiplication modulo 6. Elle définit donc bien un homomorphisme d’anneaux de $(\mathbb{Z}_6, +, \cdot)$ vers $(\mathbb{Z}_6, +, \cdot)$.