Postulado de De Zolt para las superficies

¿Qué dice el postulado de De Zolt?

Una superficie nunca puede ser equivalente a las superficies individuales (es decir, a las partes) que la componen.

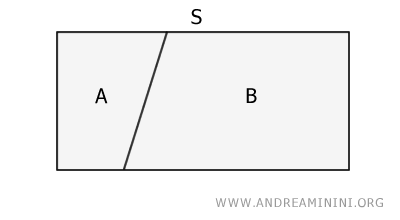
Se trata de un principio bastante intuitivo: ninguna parte de un objeto puede ser equivalente al conjunto completo.

Por eso mismo se formula como un postulado.

¿Qué es un postulado? Un postulado es un enunciado o principio que, dentro de un marco matemático o científico, se acepta como verdadero sin necesidad de demostración. Constituye un punto de partida fundamental a partir del cual se deducen, de manera lógica, teoremas y leyes posteriores.

Veamos, por ejemplo, una superficie cualquiera S.

Supongamos que trazamos una línea que divide la superficie S en dos regiones distintas, que llamaremos A y B.

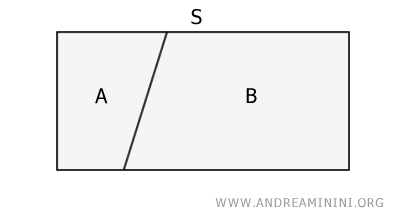
Dos superficies se consideran equivalentes si, y solo si, tienen la misma área.

En este caso, el área total de la superficie S es la suma de las áreas de A y B:

$$ Área(S) = Área(A) + Área(B) $$

Por lo tanto, ni A ni B pueden ser equivalentes a S, ni S puede ser equivalente a ninguna de sus partes.

Dicho de otro modo, una superficie nunca puede ser equivalente a una de sus partes constituyentes.

Y así sucesivamente.