Addition et soustraction d’aires

Pour additionner les aires de deux domaines, il suffit de déterminer leurs aires respectives A₁ et A₂ puis d’en effectuer la somme: A₁ + A₂. Cette méthode fonctionne tant que les domaines ne se recouvrent pas.

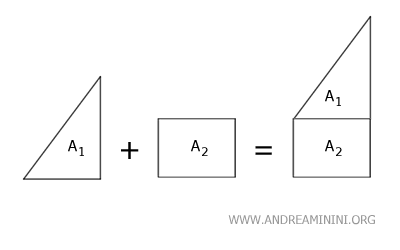
On peut procéder de la même manière pour calculer une différence d’aires: il suffit de soustraire l’aire du second domaine de celle du premier.

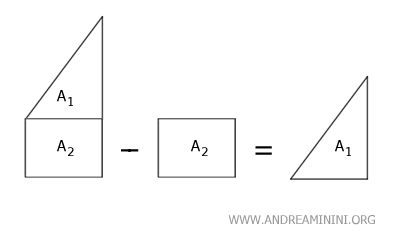
En résumé, il s’agit simplement d’additionner ou de soustraire les aires mesurées. Rien de plus.

Il est toutefois essentiel que les domaines ne se chevauchent pas. Autrement dit, ils ne doivent partager aucun point intérieur. Si un chevauchement existe, on ne peut plus additionner ou soustraire directement leurs aires sans commettre d’erreur.

Remarque: En cas de recouvrement, la zone commune ne doit être comptée qu’une seule fois dans l’aire totale. Si l’on additionne naïvement A₁ + A₂, l’intersection serait comptabilisée deux fois, ce qui fausse le résultat.

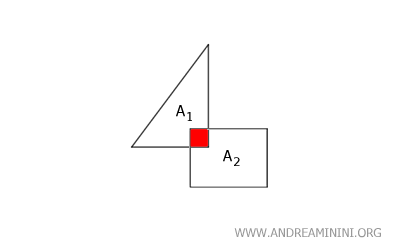
On suppose également que les deux domaines appartiennent au même plan, ce qui est le cas dans la majorité des problèmes élémentaires de géométrie.

Un exemple concret

Imaginons un premier domaine d’aire A₁ = 6 mètres carrés et un second d’aire A₂ = 12 mètres carrés.

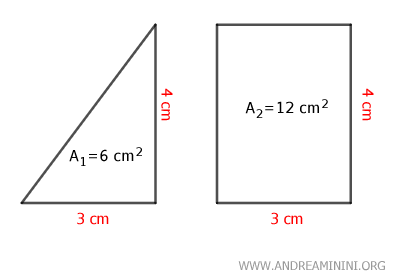
Additionnons leurs aires:

$$ A_1 + A_2 = 6 \ cm^2 + 12 \ cm^2 = 18 \ cm^2 $$

Puis calculons leur différence:

$$ A_2 - A_1 = 12 \ cm^2 - 6 \ cm^2 = 6 \ cm^2 $$

Ce résultat ne dépend absolument pas de la forme géométrique des domaines. Qu’il s’agisse de triangles, de rectangles, de disques ou de figures plus complexes, seule la valeur de leur aire intervient dans le calcul.

Observations complémentaires

Voici quelques propriétés utiles à garder en tête lorsqu’on manipule des aires:

• L’addition d’aires est commutative: $$ A_1 + A_2 = A_2 + A_1 $$
• Elle est également associative: $$ A_1 + (A_2 + A_3) = (A_1 + A_2) + A_3 $$

Ces propriétés sont fondamentales et s’appliquent à toute somme d’aires dans le plan. Elles constituent la base de nombreux raisonnements géométriques et facilitent grandement les calculs lorsque plusieurs domaines interviennent.