Théorème d’équivalence d’aire entre un triangle et un trapèze
Un trapèze est équivalent, du point de vue de l'aire, à un triangle de même hauteur (h) dont la base est égale à la somme des deux bases (B + b) du trapèze.
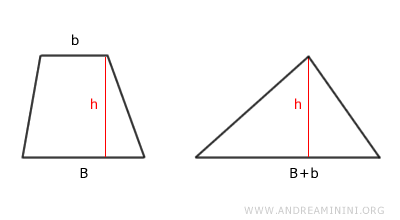
En termes simples, un triangle et un trapèze possèdent la même aire dès lors que deux conditions fondamentales sont respectées :
- leurs hauteurs sont identiques
- la base du triangle est égale à la somme des bases du trapèze
Dans ce cas, on parle de polygones équivalents.
Deux polygones sont dits équivalents lorsqu'ils peuvent être découpés et recomposés de façon à couvrir exactement la même surface, sans recouvrement ni espace vide.
Un exemple concret
Considérons un triangle et un trapèze ayant une hauteur commune h = 4.
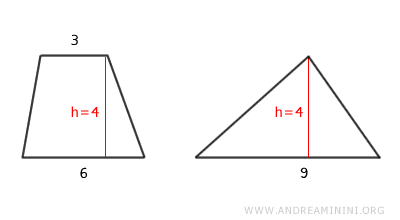
La base du triangle mesure 9. Cette valeur correspond précisément à la somme des bases du trapèze, soit 6 + 3. Le théorème d'équivalence d'aire s'applique donc immédiatement.
L'aire du triangle se calcule comme la moitié du produit de la base par la hauteur :
$$ A_t = \frac{b \cdot h}{2} = \frac{9 \cdot 4}{2} = \frac{36}{2} = 18 $$
Puisque les deux figures sont équivalentes en aire, le trapèze a la même aire :
$$ A_z = 18 $$
Aucun autre calcul n'est nécessaire.
Pour confirmer le résultat, on peut néanmoins calculer l'aire du trapèze à l'aide de la formule habituelle. L'aire est égale à la moitié du produit de la somme des bases par la hauteur. $$ A_z = \frac{(B_z + b_z) \cdot h}{2} = \frac{(6 + 3) \cdot 4}{2} = \frac{9 \cdot 4}{2} = \frac{36}{2} = 18 $$ Le résultat obtenu est le même.
Démonstration géométrique
Considérons maintenant un triangle et un trapèze dans une configuration générale :
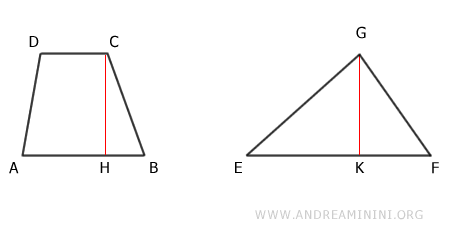
Les deux figures ont la même hauteur :
$$ \overline{CH} \cong \overline{GK} $$
De plus, la somme des bases AB et CD du trapèze est égale à la base EF du triangle :
$$ \overline{AB} + \overline{CD} \cong \overline{EF} $$
L'objectif est de montrer que ces deux figures ont la même aire.
On prolonge la grande base AB du trapèze par un segment BL, choisi de même longueur que la petite base CD :
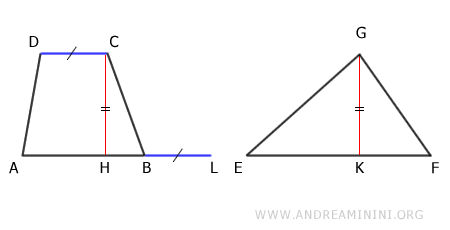
On trace ensuite le segment DL reliant les points D et L :
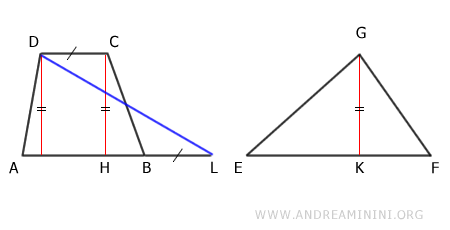
Le segment AL est alors égal à la base EF du triangle, car :
- BL ≅ CD par construction
- AB + CD ≅ EF par hypothèse, donc AB + BL ≅ EF
On obtient ainsi :
$$ \overline{AL} \cong \overline{EF} $$
D'après le critère de congruence des triangles, les triangles ADL et EFG sont congruents, puisqu'ils ont la même base et la même hauteur :
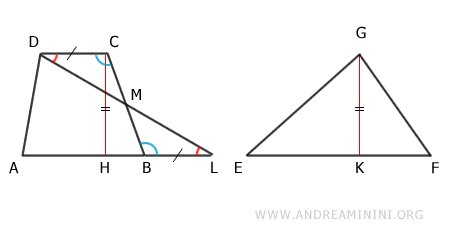
Par ailleurs, les triangles MCD et MBL sont également congruents :
- les bases du trapèze sont parallèles (AB || CD) et AL est un prolongement de AB
- BL ≅ CD par construction
- les angles correspondants sont égaux d'après le théorème des droites parallèles, angles alternes-internes
On en déduit :
$$ MCD \cong MBL $$
Des triangles congruents ayant la même aire sont également équivalents en aire :
$$ MCD \doteq MBL $$
Le trapèze ABCD peut alors être vu comme la réunion du quadrilatère ABMD et du triangle MCD :
$$ ABCD \doteq ABMD + MCD $$
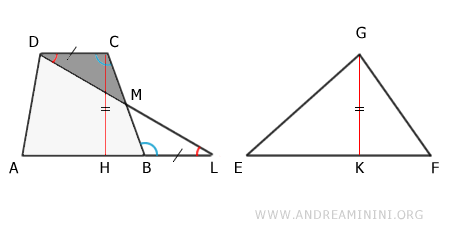
De la même manière, le triangle ADL se décompose en ABMD et en le triangle MBL :
$$ ADL \doteq ABMD + MBL $$
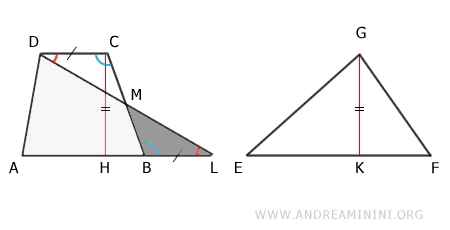
Comme MCD et MBL sont équivalents en aire, on obtient :
$$ ABCD \doteq ABMD + MCD \doteq ABMD + MBL \doteq ADL $$
Le trapèze ABCD et le triangle ADL sont donc équivalents en aire :
$$ ABCD \doteq ADL $$
Enfin, puisque le triangle ADL est congruent, et donc équivalent en aire, au triangle EFG, on conclut :
$$ ABCD \doteq ADL \doteq EFG $$
$$ ABCD \doteq EFG $$
La proposition initiale est ainsi établie.
Démonstration algébrique
Le même résultat peut être obtenu à l'aide d'un raisonnement algébrique simple.
L'aire d'un triangle est :
$$ A_t = \frac{b_t \cdot h_t}{2} $$
L'aire d'un trapèze est :
$$ A_z = \frac{(B_z + b_z) \cdot h_z}{2} $$
On cherche les conditions pour lesquelles :
$$ A_t = A_z $$
Ce qui s'écrit :
$$ \frac{b_t \cdot h_t}{2} = \frac{(B_z + b_z) \cdot h_z}{2} $$
Si les hauteurs sont égales, ht = hz :
$$ \frac{b_t \cdot h_t}{2} = \frac{(B_z + b_z) \cdot h_t}{2} $$
Si, de plus, bt = Bz + bz :
$$ \frac{b_t \cdot h_t}{2} = \frac{b_t \cdot h_t}{2} $$
L'égalité est alors immédiate : les aires sont égales.
On en conclut qu'un triangle et un trapèze sont équivalents en aire lorsqu'ils ont la même hauteur et que la base du triangle est égale à la somme des bases du trapèze.
Et ainsi de suite.