Égalité des aires d’un triangle et d’un parallélogramme

Un triangle a la même aire qu’un parallélogramme lorsque les deux figures ont la même hauteur et que la base du parallélogramme est égale à la moitié de celle du triangle.

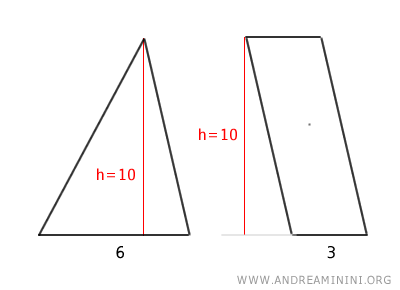
De manière équivalente, un triangle a la même aire qu’un parallélogramme qui possède la même base et une hauteur égale à la moitié de celle du triangle.

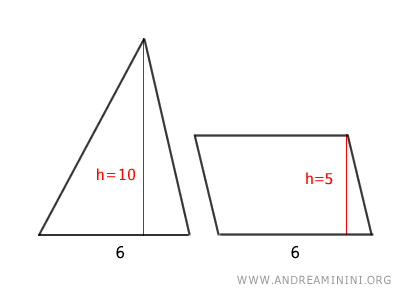
Autrement dit, lorsque le triangle et le parallélogramme ont la même hauteur et que la base du triangle est le double de celle du parallélogramme, leurs aires sont égales.

De la même façon, si les deux figures ont la même base et que la hauteur du triangle est le double de celle du parallélogramme, leurs aires coïncident également.

Un exemple numérique

Considérons un triangle et un parallélogramme.

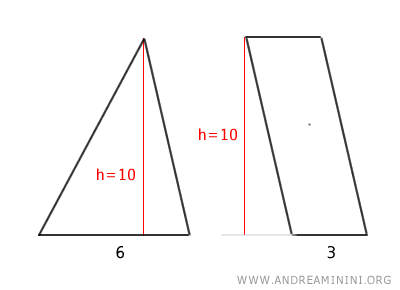
Les deux figures ont la même hauteur, h = 10.

La base du triangle mesure 6, ce qui correspond au double de la base du parallélogramme, dont la longueur est 3.

Selon la propriété d’égalité des aires, ces deux polygones ont la même aire :

$$ A_p = A_t $$

où A_p désigne l’aire du parallélogramme et A_t celle du triangle.

L’aire du parallélogramme est donnée par le produit de la base par la hauteur :

$$ A_p = 3 \cdot 10 = 30 $$

Il en résulte que l’aire du triangle vaut elle aussi :

$$ A_t = 30 $$

Exemple 2

Dans ce second exemple, le parallélogramme a la même base que le triangle (b = 6), mais sa hauteur est égale à la moitié de celle du triangle, soit h_p = 5 contre h_t = 10.

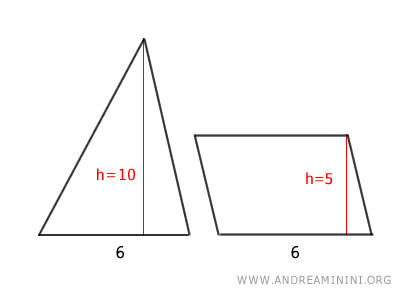
Conformément à la propriété étudiée, les deux figures ont la même aire :

$$ A_p = A_t $$

où A_p et A_t désignent respectivement les aires du parallélogramme et du triangle.

L’aire du parallélogramme est alors :

$$ A_p = 6 \cdot 5 = 30 $$

L’aire du triangle est donc également égale à :

$$ A_t = 30 $$

Démonstration

A] Parallélogramme de même hauteur et de base égale à la moitié de celle du triangle

Considérons un triangle ABC et un parallélogramme DEFG.

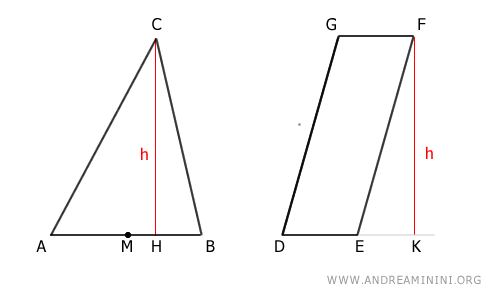
Soit M le milieu du segment AB :

$$ \overline{AM} \cong \overline{BM} $$

Par hypothèse, les hauteurs des deux figures sont égales :

$$ \overline{CH} \cong \overline{FK} $$

La base du parallélogramme est égale à la moitié de la base du triangle.

Autrement dit :

$$ \overline{AB} \cong 2 \cdot \overline{DE} $$

ce qui équivaut à :

$$ \overline{AM} \cong \overline{BM} \cong \overline{DE} $$

Il s’agit de montrer que le triangle ABC et le parallélogramme DEFG ont la même aire.

Traçons par le point M une droite parallèle au côté AC :

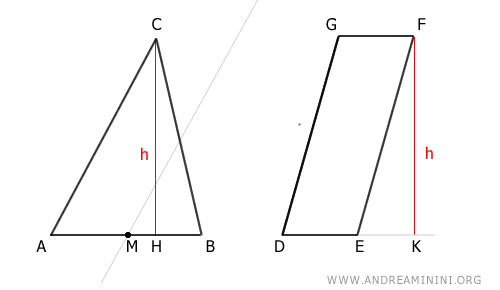
Traçons ensuite par le sommet C une droite parallèle à la base AB :

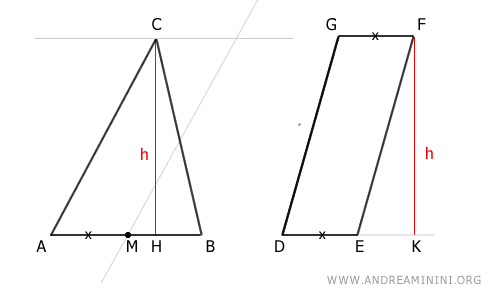
On obtient ainsi le parallélogramme AMNC :

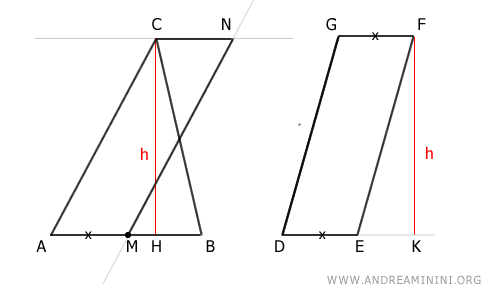
D’après le théorème d’égalité des aires des parallélogrammes, les parallélogrammes AMNC et DEFG ont la même aire, puisqu’ils ont la même base (AM ≅ DE) et la même hauteur (CM ≅ FK) :

$$ AMNC \cong DEFG $$

Les angles α ≅ δ et β ≅ γ sont égaux, car ce sont des angles alternes internes associés à des droites parallèles (théorème des droites parallèles) :

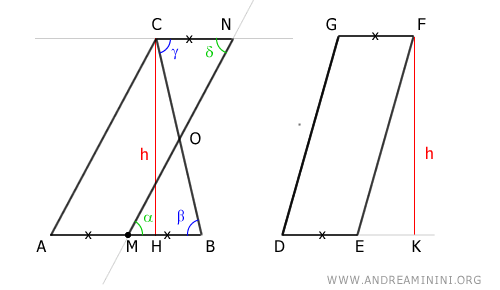
Comme BM ≅ AM puisque M est le milieu de AB, et puisque les côtés opposés d’un parallélogramme sont parallèles, on en déduit que BM ≅ CN.

Les triangles MBO et CNO sont donc congruents selon le deuxième critère de congruence des triangles :

$$ MBO \cong CNO $$

Ils ont par conséquent la même aire :

$$ MBO \doteq CNO $$

Ces aires égales sont représentées en gris :

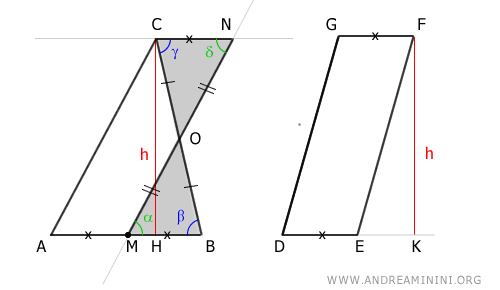
Le triangle ABC peut alors être décomposé en un trapèze AMOC et un triangle MBO :

$$ ABC \doteq AMOC + MBO $$

De même, le parallélogramme AMNC se décompose en un trapèze AMOC et un triangle CNO :

$$ AMNC \doteq AMOC + CNO $$

Comme MBO et CNO ont la même aire, on obtient :

$$ ABC \doteq AMNC $$

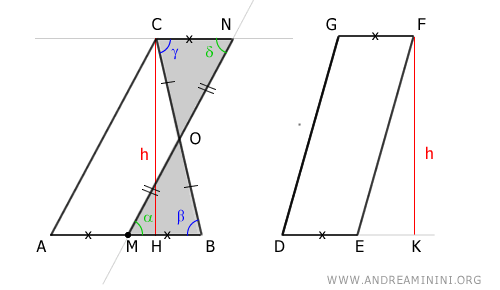
Puisque AMNC et DEFG ont la même aire, on en conclut que :

$$ ABC \doteq DEFG $$

La première partie de la démonstration est ainsi établie.

B] Parallélogramme de même base et de hauteur égale à la moitié de celle du triangle

Pour établir la seconde partie, on adopte un raisonnement algébrique.

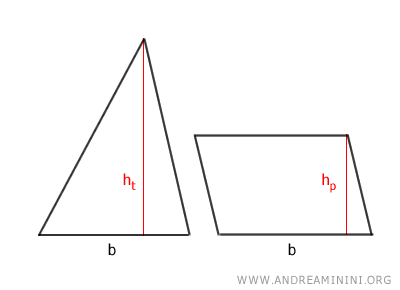
L’aire d’un triangle est donnée par la formule :

$$ A_t = \frac{b_t \cdot h_t}{2} $$

L’aire d’un parallélogramme est donnée par :

$$ A_p = b_p \cdot h_p $$

Si les bases sont égales :

$$ b_p = b_t $$

en notant cette base commune b = b_t = b_p, on obtient :

$$ A_t = \frac{b \cdot h_t}{2} $$

$$ A_p = b \cdot h_p $$

Les aires sont égales si et seulement si :

$$ \frac{b \cdot h_t}{2} = b \cdot h_p $$

En divisant chaque membre par b :

$$ \frac{h_t}{2} = h_p $$

Le parallélogramme a donc la même aire que le triangle lorsque sa hauteur est égale à la moitié de celle du triangle :

$$ h_p = \frac{h_t}{2} $$

La seconde partie de la démonstration est ainsi établie.

Remarque : le même raisonnement s’applique à la première configuration. Si les hauteurs sont égales, on a : $$ A_t = \frac{b_t \cdot h}{2} $$ $$ A_p = b_p \cdot h $$ avec h = h_t = h_p. On obtient alors : $$ \frac{b_t \cdot h}{2} = b_p \cdot h $$ d’où : $$ \frac{b_t}{2} = b_p $$ Le parallélogramme a donc la même aire que le triangle lorsque sa base est égale à la moitié de celle du triangle.

Et ainsi de suite.