Aire d’un polygone inscrit dans un cercle
Un triangle OHK et un polygone ABCDE, régulier ou irrégulier, inscrits dans un même cercle peuvent être comparés du point de vue des aires. Ils sont dits équivalents $$ ABCDE \doteq OHK $$ lorsque la hauteur du triangle est égale au rayon du cercle et que sa base correspond au périmètre du polygone.
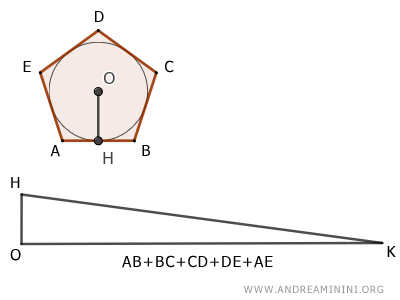
Interprété géométriquement, ce résultat montre que l'aire d'un polygone circonscrit à un cercle peut être calculée simplement en la ramenant à celle d'un triangle. Dans ce triangle de référence, la hauteur est égale au rayon du cercle et la base est égale au périmètre du polygone.
$$ Aire = \frac{\text{périmètre} \times \text{rayon}}{2} $$
Comme tout polygone régulier admet un cercle circonscrit, cette relation fournit une méthode générale pour calculer l'aire de n'importe quel polygone régulier.
À l'inverse, seuls certains polygones irréguliers possèdent un cercle circonscrit, ce qui limite l'application directe de cette méthode.
Dans la pratique, cette approche permet de simplifier considérablement les calculs. Au lieu de travailler directement sur le polygone, on se ramène au calcul de l'aire d'un triangle. La démonstration repose sur la décomposition du polygone en triangles ayant tous pour hauteur le rayon du cercle.
Un exemple
Considérons un pentagone régulier ABCDE dont chaque côté mesure 2 unités.
Ce pentagone est inscrit dans un cercle de rayon OH = 1.38.
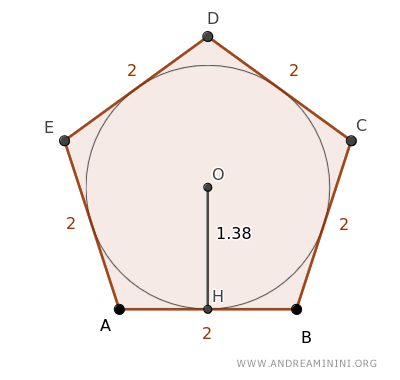
Puisqu'il s'agit d'un polygone circonscrit à un cercle, on peut utiliser directement la relation précédente pour déterminer son aire.
Le périmètre du pentagone est :
$$ P = \overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{EA} = 2 + 2 + 2 + 2 + 2 = 10 $$
On associe alors au pentagone un triangle FGI dont la base FG vaut 10, c'est-à-dire le périmètre du polygone, FG ≅ P, et dont la hauteur IF vaut 1.38, égale au rayon du cercle, IF ≅ OH.
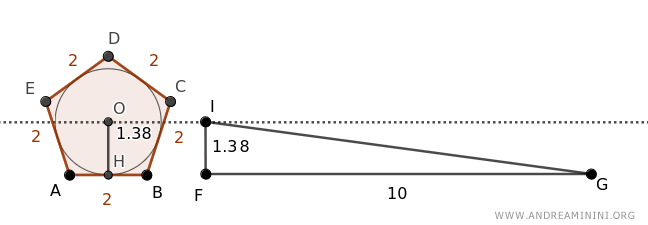
L'aire du triangle se calcule alors facilement :
$$ A_t = \frac{b \cdot h}{2} = \frac{10 \cdot 1.38}{2} = \frac{13.8}{2} = 6.9 $$
L'aire du triangle équivalent est donc :
$$ A_t = 6.9 $$
Par conséquent, l'aire du pentagone est elle aussi égale à :
$$ A_p = A_t = 6.9 $$
On obtient ainsi l'aire du pentagone sans avoir à utiliser directement une formule spécifique aux polygones réguliers.
Pour vérifier le résultat, on peut comparer avec la formule classique de l'aire d'un polygone régulier $$ A_p = \frac{n \cdot l \cdot a}{2} $$ où n = 5 est le nombre de côtés, l = 2 la longueur de chaque côté et a = 1.38 l'apotème. On obtient alors $$ A_p = \frac{5 \cdot 2 \cdot 1.38}{2} = \frac{13.8}{2} = 6.9 $$ ce qui confirme le résultat précédent.
Démonstration
Considérons un polygone ABCDE inscrit dans un cercle de centre O et de rayon OH.
Le nombre de côtés, ainsi que le fait que le polygone soit régulier ou irrégulier, n'a pas d'importance, à condition qu'il admette un cercle circonscrit.
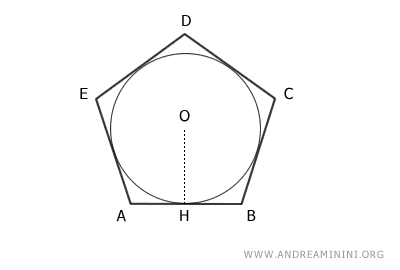
Le périmètre du polygone est donné par :
$$ P = \overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{EA} $$
En reliant le centre O à chacun des sommets du polygone, celui-ci est décomposé en plusieurs triangles.
Dans le cas présent, on obtient cinq triangles : ABO, BCO, CDO, DEO et AEO.