Parallélogrammes de même base et de même hauteur

Deux parallélogrammes sont dits équivalents lorsqu'ils ont des bases congruentes et des hauteurs correspondantes de même longueur.

Cette propriété joue un rôle central en géométrie plane. Elle permet de comparer simplement des figures de formes différentes en s'appuyant uniquement sur leur aire, sans entrer dans des calculs complexes.

Un exemple concret

Observons les deux parallélogrammes ci-dessous.

À première vue, leurs formes ne sont pas identiques. Pourtant, ils partagent la même base (b=5) et la même hauteur (h=3).

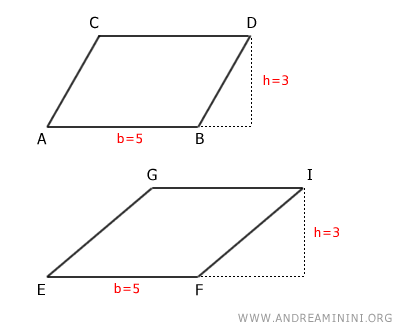
Ces deux informations suffisent pour conclure qu'ils ont la même aire.

Pour le vérifier, rappelons la formule de l'aire d'un parallélogramme :

$$ A = b \cdot h $$

où « b » représente la longueur de la base et « h » la hauteur correspondante.

$$ A = b \cdot h = 5 \cdot 3 = 15 $$

Le calcul conduit au même résultat dans les deux cas. La différence de forme n'a donc aucune incidence sur l'aire.

Démonstration

Passons maintenant à une démonstration plus générale. Considérons deux parallélogrammes, notés ABCD et EFGI.

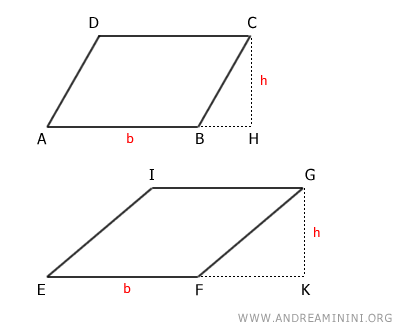
Par hypothèse, ces deux parallélogrammes ont des bases congruentes et des hauteurs correspondantes congruentes :

$$ \overline{AB} \cong \overline{EF} $$

$$ \overline{HC} \cong \overline{KG} $$

L'objectif est de montrer qu'ils ont la même aire, autrement dit qu'ils sont équivalents.

Pour cela, on fait coïncider les bases AB et EF à l'aide d'un mouvement rigide du plan, ce qui ne modifie ni les longueurs ni les aires.

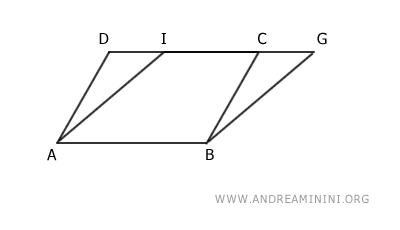
Cette superposition fait apparaître deux triangles, notés ADI et BCG.

Les angles α et β de ces triangles sont congruents. En effet, leurs côtés correspondants sont parallèles et coïncident avec des côtés de parallélogrammes, lesquels sont parallèles deux à deux par définition : AD≅BC et AI≅BG.

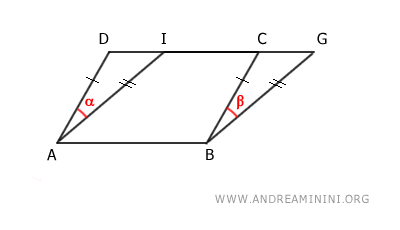
D'après le premier critère de congruence des triangles, les triangles ADI et BCG sont donc congruents, puisqu'ils possèdent deux côtés congruents et l'angle compris congruent.

$$ ADI \cong BCG $$

L'aire du parallélogramme ABCD peut alors être vue comme la différence entre l'aire du trapèze ABGD et celle du triangle BCG :

$$ ABCD \doteq ABGD - BCG $$

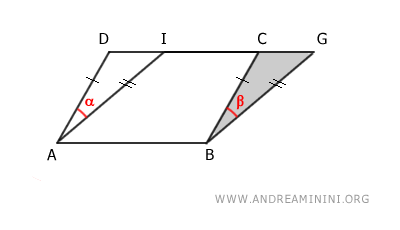
De façon analogue, l'aire du parallélogramme ABGI s'obtient en retranchant au même trapèze ABGD l'aire du triangle ADI :

$$ ABGI \doteq ABGD - ADI $$

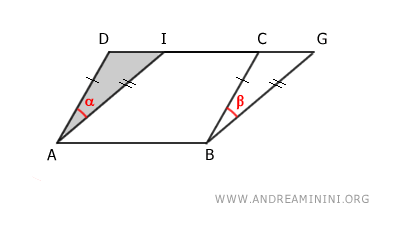
Comme les triangles ADI et BCG sont congruents, leurs aires sont égales. On en déduit que les aires des parallélogrammes ABCD et ABGI sont identiques (surfaces équivalentes), puisqu'on retranche, dans les deux cas, des triangles congruents à un même trapèze :

$$ ABCD \doteq ABGD - BCG \doteq ABGD - ADI \doteq ABGI $$

$$ ABCD \doteq ABGI $$

Enfin, les parallélogrammes ABGI et EFGI étant congruents par construction, on conclut que les parallélogrammes initiaux ABCD et EFGI sont des polygones équivalents, c'est-à-dire qu'ils possèdent exactement la même aire :

$$ ABCD \doteq EFGI $$

Remarques

Pour terminer, voici quelques remarques et prolongements naturels :

• Deux rectangles sont équivalents s'ils ont des bases et des hauteurs congruentes
  Le rectangle n'est qu'un cas particulier de parallélogramme dont les angles sont droits. La propriété établie ici s'applique donc directement aux rectangles, sans modification.

Et ainsi de suite.