Critère d’égalité des aires des triangles

Deux triangles ont la même aire lorsqu'ils possèdent des bases de même longueur et des hauteurs correspondantes égales.

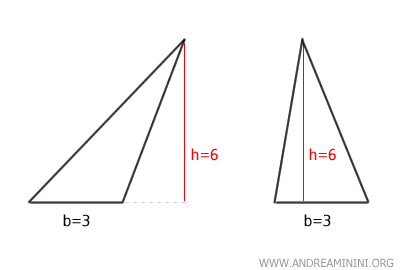
En pratique, cela signifie que la forme du triangle importe peu. Dès lors que la base et la hauteur associée sont identiques, l'aire reste la même.

Dans ce cas, les triangles sont considérés comme des polygones équivalents.

Un exemple simple

Considérons deux triangles qui ne sont pas congruents, c'est-à-dire qu'ils n'ont pas la même forme.

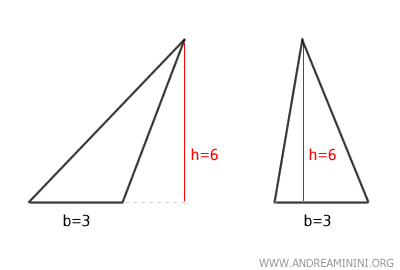
Ces deux triangles ont néanmoins la même base, b = 3, et la même hauteur, h = 6.

L'aire d'un triangle se calcule à l'aide de la formule suivante :

$$ Aire = \frac{b \cdot h}{2} $$

En remplaçant par les valeurs numériques, on obtient :

$$ Aire = \frac{3 \cdot 6}{2} = \frac{18}{2} = 9 $$

Les deux triangles ont donc une aire égale à 9. Ils sont différents par leur forme, mais équivalents du point de vue de la surface.

Démonstration

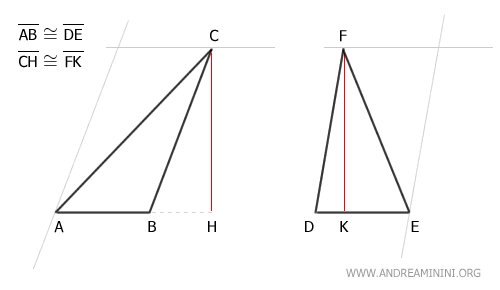
Considérons maintenant deux triangles non congruents, notés ABC et DEF.

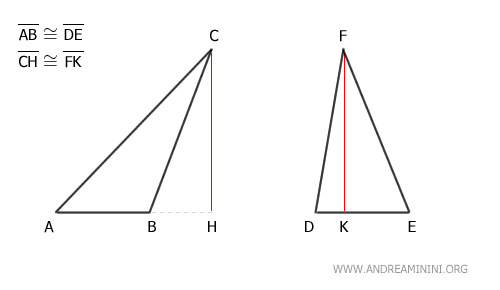
On suppose que ces deux triangles ont des bases de même longueur et des hauteurs correspondantes égales :

$$ \overline{AB} \cong \overline{DE} $$

$$ \overline{CH} \cong \overline{DK} $$

Le but est de montrer que leurs aires sont égales.

Rappelons que l'aire d'un triangle est donnée par la relation :

$$ Aire = \frac{base \cdot hauteur}{2} $$

Comme les triangles ABC et DEF ont la même base et la même hauteur, leurs aires s'écrivent :

$$ Aire (ABC) = \frac{\overline{AB} \cdot \overline{CH}}{2} $$

$$ Aire (DEF) = \frac{\overline{DE} \cdot \overline{DK}}{2} $$

Or, les longueurs correspondantes étant égales, on obtient :

$$ Aire (ABC) = Aire (DEF) $$

Les deux triangles ont donc la même aire, ce qui établit le résultat.

Démonstration alternative

Il est également possible de démontrer ce résultat à l'aide des parallélogrammes.

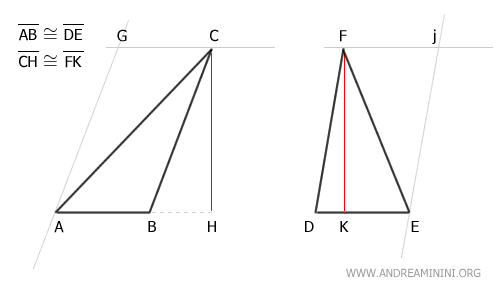
On trace des droites parallèles aux bases AB et DE passant par les sommets opposés C et F :

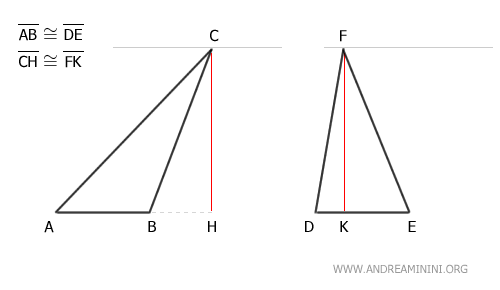
Puis, on trace des droites parallèles aux côtés BC et DF, passant elles aussi par les sommets C et F :

On obtient ainsi deux parallélogrammes, notés ABCG et DEFJ.

Chaque parallélogramme a une aire double de celle du triangle correspondant :

$$ Aire (ABCG) = 2 \cdot Aire (ABC) $$

$$ Aire (DEFJ) = 2 \cdot Aire (DEF) $$

D'après le théorème d'équivalence des parallélogrammes, ces deux parallélogrammes sont équivalents, car ils ont des bases de même longueur et des hauteurs égales.

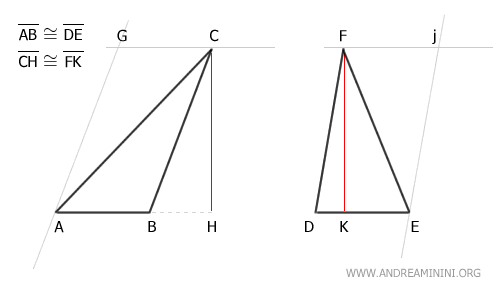
Ils ont donc des aires équivalentes :

$$ ABCG \doteq DEFJ $$

Autrement dit :

$$ Aire (ABCG) = Aire (DEFJ) $$

En divisant chaque aire par deux, on retrouve les aires des triangles correspondants :

$$ Aire (ABC) = \frac{Aire (ABCG)}{2} $$

$$ Aire (DEF) = \frac{Aire (DEFJ)}{2} $$

On en conclut que :

$$ Aire (ABC) = Aire (DEF) $$

Les triangles ABC et DEF ont donc des aires équivalentes et sont, par conséquent, équivalents du point de vue géométrique.

La proposition est ainsi démontrée.