Les surfaces en géométrie

En géométrie, une surface désigne un ensemble bidimensionnel muni d’une longueur et d’une largeur, mais dépourvu de profondeur. On peut l’imaginer comme une portion du plan que l’on découpe grâce à une ou plusieurs lignes fermées simples, qui ne se croisent jamais entre elles.

La surface fait partie des notions fondamentales de la géométrie élémentaire. Comme le point, la droite ou le plan, elle est intuitive. On ne la définit donc pas de manière entièrement formelle à ce stade, mais on l’utilise pour comprendre la structure des figures planes.

On rencontre deux grands types de surfaces: les surfaces fermées et les surfaces ouvertes.

• Surface fermée
  Une surface fermée occupe une région plane finie et est entièrement délimitée par un contour fermé. L’anneau circulaire en est un exemple clair: il est formé de deux courbes simples fermées qui ne se touchent pas. Ce type de surface possède toujours une aire que l’on peut calculer.
  
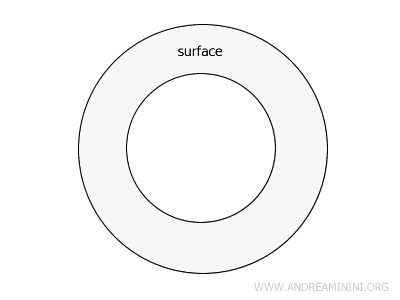
• Surface ouverte
  Une surface ouverte s’étend sans fin dans une ou plusieurs directions du plan (x;y). Le plan complet, un demi-plan ou une bande délimitée par deux droites parallèles en sont des exemples. Leur aire est infinie et échappe à toute mesure.
  

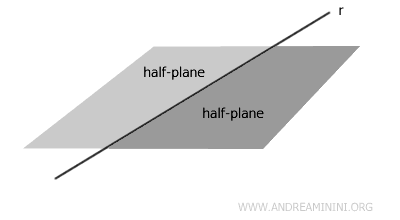
Dans la plupart des contextes, si l’on parle simplement de « surface », il s’agit d’une surface plane fermée et limitée, comme celles des figures géométriques que l’on étudie au collège ou au lycée.

Note: Une surface peut aussi être vue comme un ensemble de points dans l’espace tridimensionnel (x;y;z). Cette idée est essentielle dès que l’on cherche à mesurer la surface d’un solide. Par exemple, la surface d’un cube correspond à la somme des aires de ses six faces carrées.

Catégories de surfaces

Les surfaces peuvent être classées en deux grandes familles: les surfaces planes et les surfaces courbes. Cette distinction permet de mieux comprendre leur comportement géométrique.

• Surfaces planes
  Une surface plane est parfaitement dépourvue de courbure. Elle s’étend uniformément dans un plan unique. Elle peut être finie ou infinie. Dans une perspective plus théorique, elle correspond à l’idée abstraite du plan, qui s’étend à l’infini sans jamais se déformer.

  Une feuille de papier illustre bien ce concept, même si elle possède une épaisseur réelle. En géométrie, une surface est un objet idéal: on ne lui attribue aucune épaisseur.

• Surfaces courbes
  Une surface courbe n’est pas plane; elle présente des changements de direction ou de courbure. Elle peut être bornée ou infinie. Les surfaces courbes sont plus riches et souvent plus complexes à étudier que les surfaces planes.

  La surface d’une sphère ou la surface latérale d’un cylindre sont des exemples classiques de surfaces courbes fermées. Elles délimitent un volume dans l’espace et occupent une place fondamentale en géométrie différentielle, un domaine qui permet d’étudier les courbures avec rigueur.
  

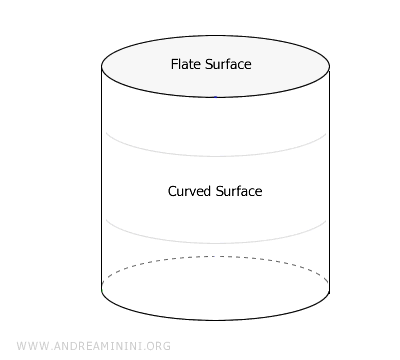
Dans les mathématiques modernes, la notion de surface dépasse largement le cadre du plan ou de l’espace tridimensionnel. Des surfaces peuvent exister dans des espaces de dimension supérieure, et même si elles sont impossibles à visualiser, elles jouent un rôle central en topologie et en géométrie avancée.

Surfaces équivalentes

On dit que deux surfaces sont équivalentes lorsqu’elles possèdent exactement la même aire.

Un triangle et un carré peuvent ainsi être équivalents si leur aire est identique, même si leurs formes n’ont rien en commun et qu’il est impossible de les superposer en utilisant uniquement des mouvements rigides.

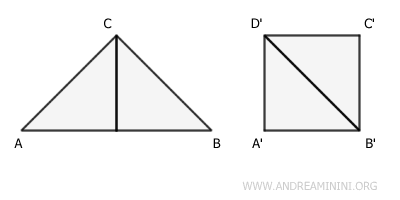
Lorsque des surfaces ont la même aire, elles appartiennent à la même classe d’équivalence définie par cette égalité.

Note: Deux figures congruentes ont toujours la même aire. En revanche, deux figures de même aire ne sont pas forcément congruentes, un point crucial lorsqu’on étudie la classification des figures planes.

Somme et différence de surfaces

Si deux surfaces S₁ et S₂ n’ont aucun point commun, leur aire totale s’obtient simplement en additionnant leurs aires: Aire(S₁)+Aire(S₂).

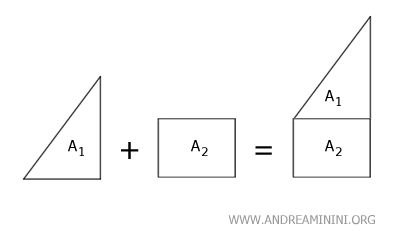
La différence entre deux surfaces disjointes se calcule tout aussi directement: Aire(S₁) - Aire(S₂).

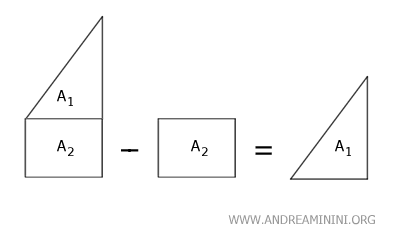
Comparer des surfaces

La comparaison entre surfaces repose presque toujours sur leur aire. On peut rencontrer plusieurs situations.

• Surfaces équivalentes
  Elles ont exactement la même aire.
  
• Surface plus grande
  Une surface est plus grande qu’une autre si son aire est strictement supérieure. Elle occupe alors davantage d’espace.
  
• Surface plus petite
  Une surface est plus petite si son aire est strictement inférieure à celle d’une autre.
  

Ces notions constituent la base de nombreuses comparaisons en géométrie. Elles permettent de comprendre non seulement la taille des figures mais aussi la manière dont elles peuvent être transformées, découpées ou recomposées.