Relația inversă

Fie o relație aRb definită pe produsul cartezian A×B. Relația inversă bR^-1a este submulțimea lui B×A care conține toate perechile (b, a) pentru care se verifică aRb.

Cu alte cuvinte, dacă aRb reprezintă o relație de la mulțimea A la mulțimea B, atunci relația inversă bR^-1a stabilește o corespondență de la B înapoi către A.

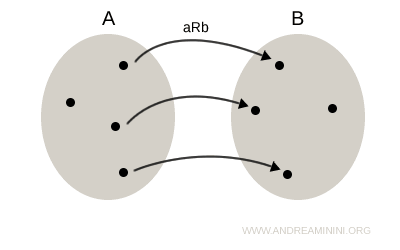
Relația inversă R^-1 se obține prin inversarea ordinii fiecărei perechi (a, b), rezultând perechea (b, a).

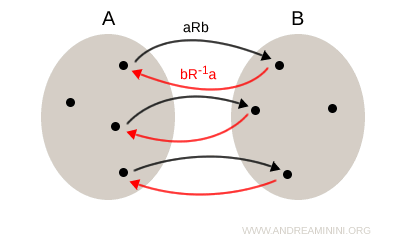
Reprezentarea grafică a relației inverse se face prin schimbarea sensului săgeților: pentru fiecare săgeată aRb orientată de la A către B, există o săgeată bR^-1a orientată de la B către A.

În consecință, domeniul relației inverse coincide cu codomeniul relației inițiale:

$$ \text{domeniul} \ R^{-1} = \text{codomeniul} \ R $$

Iar codomeniul relației inverse coincide cu domeniul relației inițiale:

$$ \text{codomeniul} \ R^{-1} = \text{domeniul} \ R $$

Notă: Relația inversă bR^-1a este adevărată dacă și numai dacă este adevărată relația inițială aRb. $$ bR^{-1}a \Leftrightarrow aRb $$

Un exemplu practic

Să considerăm două mulțimi finite A și B:

$$ A = \{2,3,4,5,6 \} $$

$$ B = \{4,9,16,25,36 \} $$

Relația R asociază fiecărui element din A pătratul său din B:

$$ aRb \ : \ b = a^2 $$

Această relație este o submulțime a produsului cartezian A×B și este alcătuită din următoarele perechi ordonate (a, b):

$$ aRb = \{ (2,4), (3,9), (4,16), (5,25), (6,36) \} \subset A×B $$

Diagrama sagitală de mai jos reprezintă relația aRb:

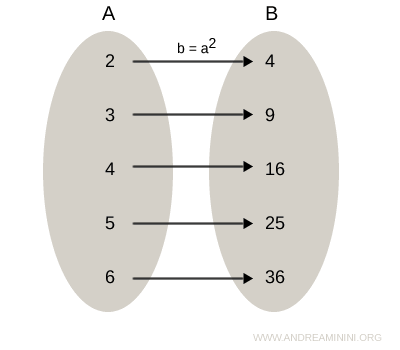
Relația inversă R^-1 asociază fiecărui element din B rădăcina pătrată corespunzătoare din A, adică perechile inverse (b, a):

$$ R^{-1} = \{ (4,2), (9,3), (16,4), (25,5), (36,6) \} \subset B×A $$

Astfel, diagrama sagitală a relației inverse se obține schimbând sensul tuturor săgeților: dinspre B către A.