Relații antisimetrice

Ce este o relație antisimetrică?

O relație definită pe o mulțime X se numește antisimetrică dacă, pentru orice pereche de elemente distincte, din faptul că a se află în relație cu b rezultă că b nu se află în relație cu a: $$ a R b \ ,\ a \ne b \ \Rightarrow b \require{cancel} \cancel{R} a $$

Cu alte cuvinte, într-o relație antisimetrică niciun cuplu de elemente distincte nu poate fi legat în ambele sensuri.

De pildă, relația „A este mai mare sau egal cu B” este antisimetrică: dacă A ≥ B și A ≠ B, atunci nu poate fi adevărat și B ≥ A.

Această proprietate permite reciprocitatea exclusiv atunci când elementele coincid.

Diferența dintre antisimetrie și asimetrie. Deși la prima vedere par apropiate, cele două concepte descriu situații distincte. Într-o relație antisimetrică, reciprocitatea este admisă numai între elemente identice. Într-o relație asimetrică, orice formă de reciprocitate este exclusă, inclusiv între elemente egale. De exemplu, relația „mai mare sau egal cu” este antisimetrică: dacă A ≥ B și A ≠ B, atunci nu poate avea loc B ≥ A. Totuși, aceeași relație nu este asimetrică, deoarece pentru A = B sunt adevărate atât A ≥ B, cât și B ≥ A, ceea ce generează o pereche simetrică.

Relațiile antisimetrice constituie o subclasă a relațiilor definite pe o mulțime.

Un exemplu concret

Să considerăm mulțimea:

$$ I = \{ 1, 2, 3, 4 \} $$

Definim relația R ca „x este mai mare sau egal cu y”:

$$ R = \{ (4;3), (4;2), (4;1), (3;2), (3;1), (2;1) \} $$

Această relație este antisimetrică, deoarece pentru orice pereche de elemente distincte x și y, dacă x ≥ y, atunci y ≥ x nu este adevărat.

Notă. De exemplu, 4 ≥ 3: $$ 4 > 3 $$ iar reciproca 3 ≥ 4 este falsă: $$ 3 < 4 $$ Prin urmare, relația respectă condiția de antisimetrie.

Într-o reprezentare grafică, niciun cuplu de noduri distincte nu apare conectat prin muchii orientate în ambele direcții.

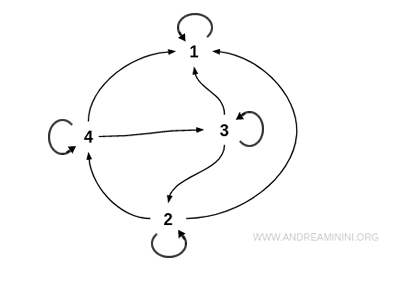
Singurele legături bidirecționale sunt buclele, care exprimă faptul că un element este în relație cu el însuși - de exemplu, 3 ≥ 3.

Spre deosebire de relațiile asimetrice, buclele sunt perfect compatibile cu antisimetria.

Aceasta deoarece antisimetria privește exclusiv raporturile dintre elemente distincte.

Observații suplimentare

Câteva aspecte importante despre relațiile antisimetrice:

• O relație poate să nu fie nici simetrică, nici antisimetrică. Aceste proprietăți nu sunt nici exclusive, nici exhaustive.

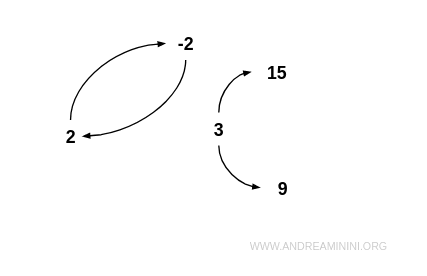
  Exemplu. Considerăm mulțimea $$ I = \{ -2, 2, 3, 9, 15 \} $$ și relația R definită ca „x este un divizor propriu al lui y”: $$ R = \{ (-2;2), (2;-2), (3;9), (3;15) \} $$ Această relație nu este antisimetrică, întrucât -2 și 2 sunt legate reciproc. Nu este însă nici simetrică, pentru că 9 nu este divizor al lui 3. Prin urmare, R nu este nici simetrică, nici antisimetrică. În graful asociat, se observă o muchie bidirecțională între -2 și 2, dar nu între toate perechile de noduri.
  

Și așa mai departe.