Relații Reflexive
Ce este o relație reflexivă?
O relație definită pe o mulțime A se numește reflexivă dacă fiecare element al lui A este în relație cu el însuși. $$ \forall \ a \in A \ , \ aRa $$
Cu alte cuvinte, o relație reflexivă stabilește, pentru fiecare element al mulțimii, o legătură cu el însuși.
De pildă, relația „X are aceeași vârstă cu Y” este reflexivă, deoarece orice persoană are, în mod firesc, aceeași vârstă cu ea însăși.
Relațiile reflexive fac parte din categoria mai generală a relațiilor definite pe o mulțime.
Un Exemplu Concret
Considerăm mulțimea A:
$$ A = \{ 2,3,4,5,6,7,8,9 \} $$
Definim o relație R care asociază fiecărui element multiplii săi, cu condiția ca aceștia să aparțină tot mulțimii A.
$$ R = \{ (2;2), (2;4), (2;6), (2;8), (3;3), (3;6), (3;9)\\ \ \ \ \ \ \ \ \ \ \ \ \ (4;4), (4;8), (5;5), (6;6), (7;7), (8;8), (9;9) \} $$
Această relație este așadar o submulțime a produsului cartezian A × A, adică a tuturor perechilor ordonate de elemente din A.
Relația poate fi ilustrată printr-un tabel cu dublă intrare:
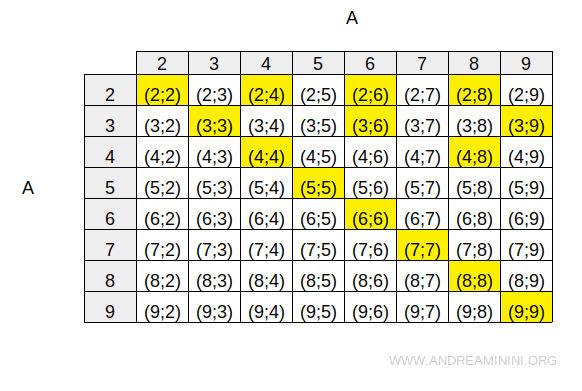
Celulele colorate în galben marchează perechile din produsul A×A care satisfac relația R.
Se observă că fiecare element este în relație cu el însuși.
Diagonala principală a tabelului conține doar perechi de forma (a,a), care aparțin relației și sunt evidențiate în galben: (2;2), (3;3), (4;4) ș.a.m.d.
Aceasta confirmă că R este, într-adevăr, o relație reflexivă.
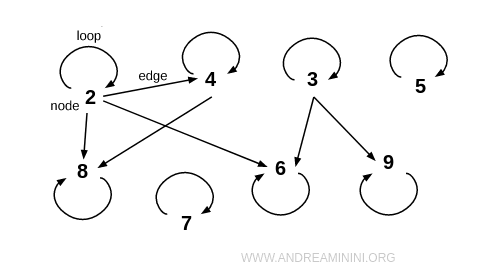
Notă. Într-o reprezentare prin graf, o relație este reflexivă dacă fiecare nod are un buclaj, adică o muchie orientată care îl leagă de el însuși. Această caracteristică vizuală permite recunoașterea reflexivității dintr-o privire.
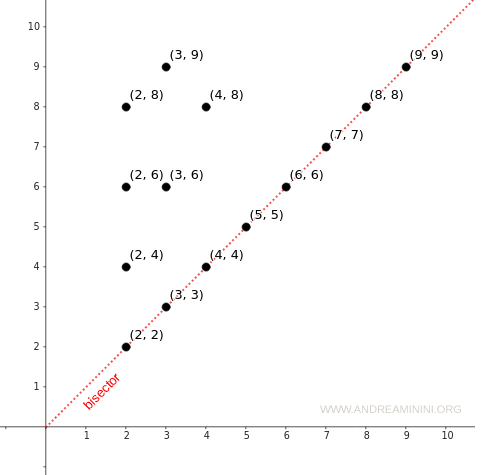
Într-o reprezentare carteziană, reflexivitatea se traduce prin apariția tuturor punctelor (a,a) pe diagonala principală (bisectoare). Și aici, proprietatea se identifică imediat.
Alte Exemple
- Relația „x este perpendiculară pe y” nu este reflexivă, deoarece nicio dreaptă nu poate forma un unghi drept cu ea însăși.
Și așa mai departe.