Relații Matematice

Ce este o relație?

O relație reprezintă o regulă prin care anumite elemente din mulțimea A sunt asociate cu unul sau mai multe elemente din mulțimea B. $$ aRb $$ Unde a∈A și b∈B, iar elementul b se numește imaginea lui a.

Merită subliniat faptul că am folosit cuvântul „anumite” elemente, deoarece regula nu trebuie neapărat să se aplice tuturor elementelor din A.

În același mod, nu este obligatoriu ca relația să includă toate elementele din B.

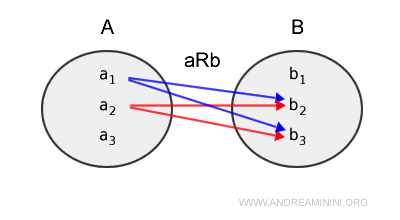
De asemenea, un singur element din A poate fi asociat cu mai multe elemente din B.

Diagrama lui Venn prezentată mai sus poate fi redată și astfel:

Așadar, o relație nu este altceva decât o submulțime a produsului cartezian AxB dintre cele două mulțimi.

$$ R \subseteq AxB $$

Notă. Când mulțimea A coincide cu mulțimea B, adică A=B, spunem că relația matematică este definită pe A.

Un Exemplu Practic

Să considerăm două mulțimi, A și B:

$$ A = \{ 2, 4, 6, 8 \} \\ B = \{ 1, 3, 5 \} $$

Produsul cartezian AxB este format din toate perechile ordonate (a,b), unde a∈A și b∈B.

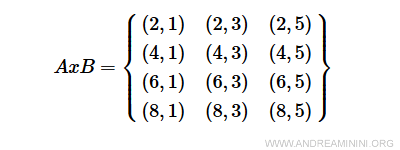
Definim acum o relație R care leagă perechile (a,b) pentru care condiția a+2b<10 este îndeplinită.

De pildă, perechea (a,b)=(2,1) aparține lui R, deoarece 2+2·1=4<10.

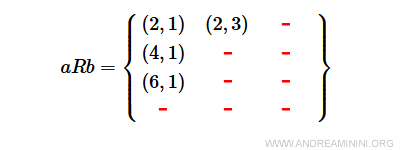
Notă. Orice pereche (a,b) face parte din produsul cartezian AxB; prin urmare, o relație este de fapt o submulțime a acestuia.

Relația R selectează doar anumite perechi din AxB.

În acest caz, perechile (2,1), (2,3), (4,1) și (6,1) satisfac condiția impusă de R, în timp ce restul nu.

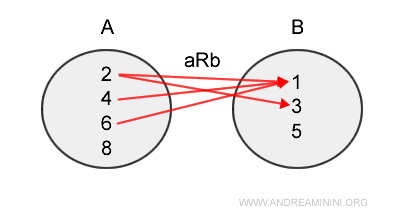
Prin urmare, submulțimea aRb este alcătuită din patru elemente:

$$ aRb = \{ (2,1), (2,3), (4,1) , (6,1) \} \subset AxB $$

Notă. Între mulțimile A și B se pot defini un număr infinit de relații; aceasta este doar una dintre ele. De exemplu, dacă definim o altă relație R' prin condiția 2a+b<10, atunci submulțimea aR'b va fi complet diferită: $$ aR'b = \begin{Bmatrix} (2,1) & ( 2,3 ) & (2,5) \\ (4,1) & - & - \\ - & - & - \\ - & - & - \end{Bmatrix} $$

Exemplu

Să revenim la mulțimile A și B și la relația R: a+2b<10.

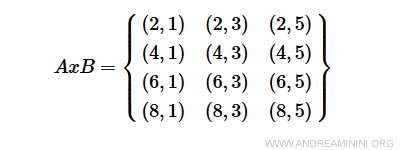
Elementele din A care respectă relația sunt 2, 4 și 6.

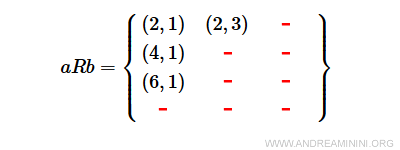
Astfel, domeniul lui R este format din elementele 2, 4 și 6 ale mulțimii A, iar codomeniul lui R din elementele 1 și 3 ale mulțimii B.

$$ \text{dom(R)} = \{2, 4, 6 \} $$

$$ \text{codom(R)} = \{1,3 \} $$

Notă. În unele lucrări de matematică, domeniul este considerat întreaga mulțime A, fără a se distinge între elementele care au imagine în B prin R și cele care nu au. În acest caz, domeniul ar fi întreaga mulțime A: $$ \text{dom(R)} = \{2, 4, 6, 8 \} $$ Submulțimea lui A pe care este efectiv definită relația R se numește mulțimea de definiție sau câmpul de existență al lui R: $$ \text{mulțimea de definiție} = \{2, 4, 6 \} $$

Reprezentarea unei Relații

O relație binară între două mulțimi poate fi reprezentată în mai multe moduri:

• Reprezentare prin enumerare
  Se scriu explicit perechile ordonate (a,b) care satisfac relația. $$ aRb = \{ (2,1), (2,3), (4,1), (6,1) \} $$
• Diagrama cu săgeți
  Este reprezentarea grafică tradițională a unei relații, în care săgețile unesc elementele lui A cu elementele corespunzătoare din B.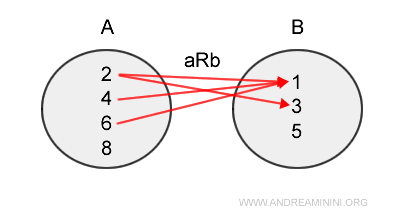

  

• Matricea relației (sau tabel cu dublă intrare)
  Relația poate fi redată și printr-o matrice a relației, în care elementele lui A apar pe linii, iar cele ale lui B pe coloane. În fiecare celulă se notează:
  • 1 dacă perechea (a,b) aparține relației R;
  • 0 dacă perechea (a,b) nu aparține lui R.

  Exemplu practic. Produsul cartezian AxB este:
  
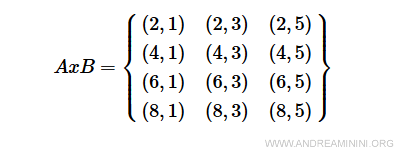
  Relația aRb definită prin condiția a+2b<10 se reprezintă prin următoarea matrice a relației, în care elementele lui A se află pe linii, iar cele ale lui B pe coloane. $$ aRb = \begin{Bmatrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{Bmatrix} $$ Pentru o prezentare mai intuitivă, se poate folosi și un tabel cu dublă intrare.
  

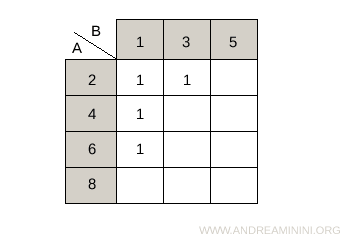
• Reprezentare carteziană
  Într-un plan cartezian, elementele lui A (domeniul) se reprezintă pe axa orizontală, iar cele ale lui B (codomeniul sau imaginea) pe axa verticală. Fiecare punct din plan corespunde unei perechi ordonate (a,b) care respectă relația.
  

   

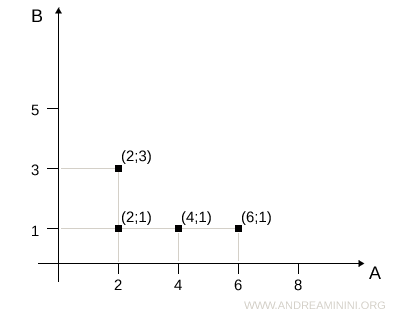
Relația Inversă

Dacă avem o relație \( b=R(a) \), atunci relația inversă \( a=R^{-1}(b) \) stabilește corespondențe între elementele mulțimii B și cele ale mulțimii A.

Relația inversă \( bR^{-1}a \) există dacă și numai dacă există relația \( aRb \).

$$ bR^{-1}a \Leftrightarrow aRb $$

În consecință, domeniul relației inverse \( R^{-1} \) coincide cu codomeniul relației \( R \):

$$ dom \ R^{-1} = codom \ R $$

Iar codomeniul lui \( R^{-1} \) coincide cu domeniul lui \( R \):

$$ codom \ R^{-1} = dom \ R $$

Exemplu practic

Să reluăm mulțimile A și B împreună cu relația R: a+2b<10.

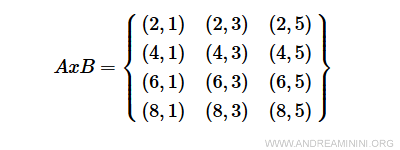
Elementele din A care respectă relația sunt 2, 4 și 6.

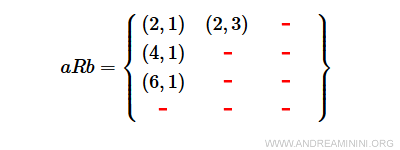
Relația de la A la B este:

$$ aRb = \{ (2,1), (2,3), (4,1) , (6,1) \} \subset AxB $$

Relația inversă de la B la A este:

$$ bR^{-1}a = \{ (1,2), (3,2), (1,4) , (1,6) \} \subset BxA $$

Observăm că relația inversă are direcția opusă celei inițiale.

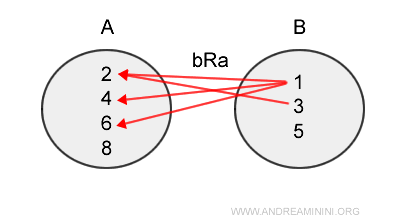
Notă. În relația \( aRb \), perechile sunt de forma (a,b). În relația inversă ordinea se inversează: (b,a).

Tipuri de Relații

Relațiile se pot clasifica în mai multe categorii:

• Funcții (sau aplicații)
• Relații binare
  O relație binară între două mulțimi A și B este o submulțime a produsului cartezian AxB. Se notează astfel: $$ aRb \ \ a \in A, \ \ b \in B $$ Este numită binară pentru că pune în corespondență elemente din două mulțimi, formând perechi ordonate (a,b): $$ (a,b) \in aRb $$
• Relații de ordine
  Acestea respectă proprietățile de reflexivitate, antisimetricitate și tranzitivitate.
• Relații de echivalență
  Acestea respectă proprietățile de reflexivitate, simetrie și tranzitivitate.
• Relații de compatibilitate
  Sunt reflexive și simetrice, dar nu sunt tranzitive.

Fiecare tip de relație se caracterizează printr-un set specific de proprietăți.

• O relație este reflexivă dacă $$\forall a \in A \Rightarrow (a,a) \in R $$
• O relație este simetrică dacă $$ \forall (a,b) \in R \Rightarrow (b,a) \in R $$
• O relație este antisimetrică dacă $$ \forall (a,b) \in R \ \text{și} \ (b,a) \in R \Rightarrow a=b $$
• O relație este tranzitivă dacă $$ \forall (a,b) \in R, \ (b,c) \in R \Rightarrow (a,c) \in R $$

Proprietățile de reflexivitate, simetrie și tranzitivitate sunt independente unele de altele, astfel încât o relație poate îndeplini unele dintre ele, dar nu neapărat pe toate.