Relații simetrice

Ce este o relație simetrică?

O relație se numește simetrică dacă, de fiecare dată când un element a este în relație cu un element b, atunci și b se află în relație cu a. $$ \forall a,b \in X \ , \ aRb \Rightarrow bRa $$

Sunt denumite „simetrice” deoarece, atunci când sunt reprezentate grafic, prezintă o structură cu aspect de oglindă.

De exemplu, dacă X este fratele lui Y, atunci și Y este fratele lui X.

Relațiile simetrice formează o subclasă a relațiilor definite pe o mulțime.

Notă. O relație simetrică face parte din relațiile de echivalență dacă este totodată reflexivă și tranzitivă.

Un exemplu practic

Să considerăm mulțimea:

$$ A = \{ -1, -2, -3, 1, 2, 3 \} $$

Definim o relație R care asociază fiecare număr cu opusul său aditiv.

$$ R = \{ (-1;1), (-2;2), (-3;3), (1;-1), (2;-2), (3;-3) \} $$

Această relație este o submulțime a produsului cartezian A� - A.

O putem reprezenta printr-un tabel cu dublă intrare.

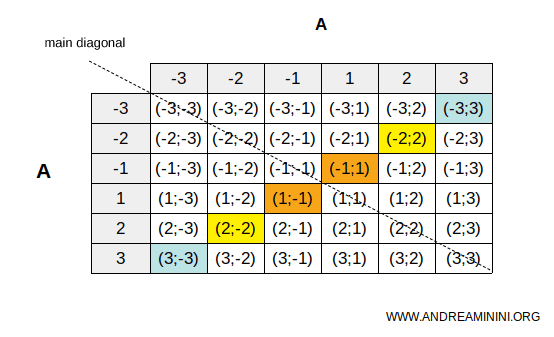
Tabelul evidențiază o simetrie evidentă față de diagonala principală.

Pentru fiecare celulă care verifică relația (marcată în culoare), există imaginea ei în oglindă față de diagonală, care face la rândul ei parte din relație: ambele sunt evidențiate identic.

De exemplu, -2 este opusul lui 2, iar 2 este opusul lui -2.

Această simetrie devine și mai vizibilă dacă reprezentăm relația în planul cartezian.

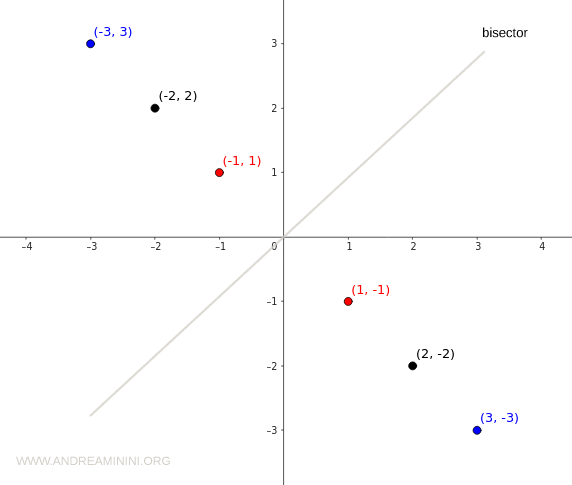
În acest caz, simetria se reflectă pe bisectoare.

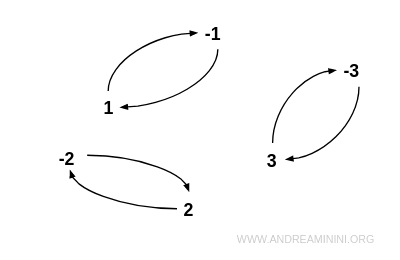
Notă. Într-o reprezentare grafică a unei relații simetrice, fiecărei muchii orientate dintr-un vârf în altul îi corespunde o muchie orientată în sens invers.

Alte exemple

• Relația „x este perpendiculară pe y” este simetrică, deoarece dacă o dreaptă x este perpendiculară pe y, atunci și y este perpendiculară pe x.

Observații suplimentare

Câteva aspecte esențiale despre relațiile simetrice:

• Faptul că o relație nu este simetrică nu înseamnă că este asimetrică: există relații care nu sunt nici simetrice, nici asimetrice.
• Simetria nu este opusul antisimetriei; de fapt, o relație poate să nu posede niciuna dintre cele două proprietăți.

Și așa mai departe.