Relații asimetrice

Ce este o relație asimetrică?

O relație definită pe o mulțime X se numește asimetrică dacă, ori de câte ori un element a se află în relație cu un element b, atunci b nu se află în relație cu a. $$ a R b \ \ \Rightarrow b \require{cancel} \cancel{R} a $$

Într-o relație asimetrică, niciun cuplu de elemente distincte nu poate fi legat reciproc.

De exemplu, relația „A este mama lui B” este asimetrică: dacă A este mama lui B, atunci B nu poate fi mama lui A.

Relațiile asimetrice fac parte din categoria mai generală a relațiilor definite pe o mulțime.

Un exemplu practic

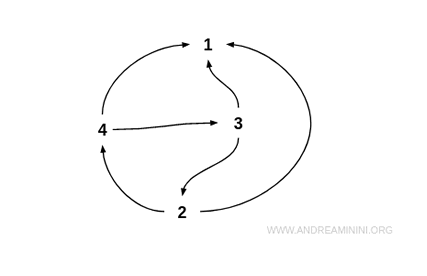
Să considerăm mulțimea:

$$ I = \{ 1, 2, 3, 4 \} $$

Definim R ca relația „x este mai mare decât y”:

$$ R = \{ (4;3), (4;2), (4;1), (3;2), (3;1), (2;1) \} $$

Această relație este asimetrică, deoarece dacă x este mai mare decât y, atunci y nu poate fi mai mare decât x.

Notă. De exemplu, 4 este mai mare decât 3: $$ 4 > 3 $$ dar 3 nu este mai mare decât 4: $$ 3 < 4 $$ Prin urmare, relația respectă condiția de asimetrie.

Într-o reprezentare prin graf, o relație asimetrică nu conține muchii orientate în ambele sensuri între niciun cuplu de noduri distincte.

Asimetrie vs. Antisimetrie

Noțiunile de asimetrie și antisimetrie sunt adesea confundate, deși descriu proprietăți diferite.

• Relație antisimetrică
• Într-o relație antisimetrică, două elemente pot fi în relație reciprocă numai dacă sunt identice. Formal: dacă \( aRb \) și \( bRa \), atunci \( a = b \). Cu alte cuvinte, dacă \( a \ne b \), atunci \( b \not\!Ra \). $$ aRb ,\ a \ne b \ \Rightarrow b \require{cancel} \cancel{R} a $$
• Relație asimetrică
• O relație asimetrică, în schimb, interzice orice formă de reciprocitate, inclusiv între elemente identice. Nici măcar perechea \( (a,a) \) nu poate aparține relației. $$ aRb \ \ \Rightarrow b \require{cancel} \cancel{R} a $$

Pe scurt: antisimetria permite reciprocitatea doar când elementele coincid, în timp ce asimetria o exclude complet.

Observații suplimentare

Câteva aspecte esențiale privind relațiile asimetrice:

• Nu toate relațiile sunt simetrice sau asimetrice. Faptul că o relație nu este asimetrică nu implică automat că este simetrică, și invers.

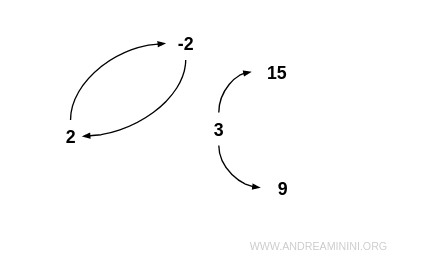
  Exemplu. Considerăm mulțimea $$ I = \{ -2, 2, 3, 9, 15 \} $$ și relația R definită prin „x este un divizor propriu al lui y”: $$ R = \{ (-2;2), (2;-2), (3;9), (3;15) \} $$ Această relație nu este asimetrică, deoarece -2 și 2 sunt în relație în ambele sensuri. Nu este însă nici simetrică, întrucât nu toate perechile sunt reciproce: de exemplu, 3 este în relație cu 9, dar 9 nu este în relație cu 3. Prin urmare, R nu este nici simetrică, nici asimetrică. În graful corespunzător, există o muchie bidirecțională între -2 și 2, dar nu între toate perechile de noduri.
  

Și așa mai departe.