Relații ireflexive
Ce înseamnă o relație ireflexivă?
O relație definită pe o mulțime I se numește ireflexivă (sau antireflexivă) dacă niciun element al mulțimii nu se află în relație cu el însuși. $$ \forall \ a \in I \ , \ a \require{cancel} \cancel{R} a $$
Într-o relație ireflexivă, absolut niciun element nu este raportat la sine însuși.
De exemplu, relația „A este mama lui B” este ireflexivă, pentru că nimeni nu poate fi propria sa mamă.
Relațiile ireflexive constituie o subclasă particulară a relațiilor definite pe o mulțime.
Un exemplu practic
Considerăm mulțimea finită I:
$$ I = \{ 2,4,3,9,16 \} $$
Definim o relație R care pune în corespondență fiecare element cu rădăcina sa pătrată; adică: „x este rădăcina pătrată a lui y”.
$$ R = \{ (4;2), (16;4), (9;3) \} $$
Această relație este ireflexivă deoarece niciun element al mulțimii I nu este rădăcina pătrată a lui însuși.
Notă. De pildă, 2 nu este rădăcina pătrată a lui 2. $$ 2 \ne \sqrt{2} $$ Același lucru este valabil pentru toate celelalte elemente din I. Într-o reprezentare sub formă de graf, o relație ireflexivă se caracterizează prin absența completă a buclelor: niciun nod nu este conectat la sine.
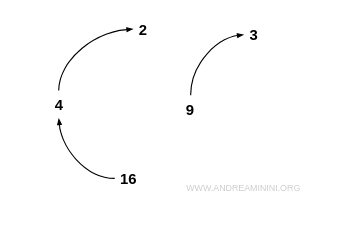
Observații suplimentare
Câteva aspecte esențiale privind relațiile ireflexive:
- Există relații care nu sunt nici reflexive, nici ireflexive. Cu alte cuvinte, faptul că o relație nu este ireflexivă nu implică automat că ar fi reflexivă, și invers.
Exemplu. Considerăm mulțimea $$ I = \{1,2,3,4,9,16 \} $$ și relația R definită prin „x este rădăcina pătrată a lui y”. Această relație nu este reflexivă, pentru că nu toate elementele se raportează la ele însele - de exemplu, 2 nu este rădăcina pătrată a lui 2. $$ 2 \ne \sqrt{2} $$ Dar nici ireflexivă nu este, fiindcă include cel puțin o pereche reflexivă: de exemplu, 1 este rădăcina pătrată a lui 1. $$ 1 = \sqrt{1} $$ În graful corespunzător acestei relații, nodul 1 are o buclă. Aceasta arată că relația nu este ireflexivă. Totuși, deoarece nu toate nodurile au bucle, relația nu este nici reflexivă.
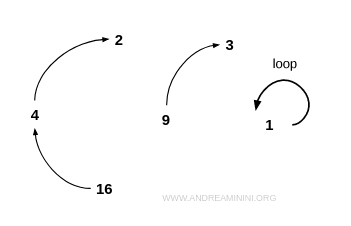
Și așa mai departe.