Relații tranzitive
Ce este o relație tranzitivă?
O relație se numește tranzitivă dacă, pentru orice trei elemente a, b și c dintr-o mulțime I, atunci când a este în relație cu b, iar b este în relație cu c, rezultă în mod necesar că și a este în relație cu c. $$ \forall \ a,b,c \in I \ | \ aRb \ , \ bRc \ \Rightarrow aRc $$ Această proprietate poate fi ilustrată grafic astfel:
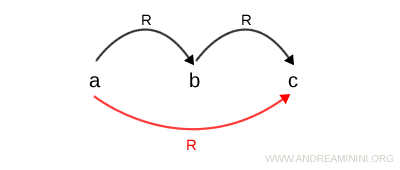
Se numesc tranzitive deoarece respectă proprietatea tranzitivității.
De pildă, dacă A este fratele lui B și B este fratele lui C, atunci A este, la rândul său, fratele lui C.
Relațiile tranzitive fac parte din categoria mai generală a relațiilor definite pe o mulțime.
Notă: Nu toate relațiile sunt tranzitive. Spre exemplu, dacă A este mama lui B și B este mama lui C, nu rezultă că A este și mama lui C; prin urmare, această relație nu este tranzitivă.
Un exemplu practic
Considerăm mulțimea I:
$$ I = \{ 2 , 4, 6, 8, 10 \} $$
Relația R pune în corespondență numerele pare din această mulțime.
De exemplu, 2 și 4 se află în relație pentru că ambele sunt numere pare:
$$ 2R4 $$
La fel, și 4 și 6 sunt în relație din același motiv:
$$ 4R6 $$
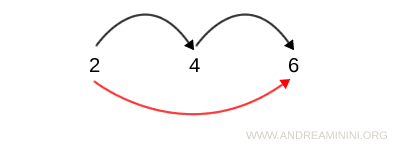
Aplicând proprietatea tranzitivității, rezultă că 2 și 6 trebuie să fie în relație: dacă 2 este legat de 4, iar 4 este legat de 6, atunci 2 este legat și de 6:
$$ 2R6 $$
În acest caz, proprietatea tranzitivității este valabilă pentru toate combinațiile posibile de elemente ale mulțimii I = {2, 4, 6, 8, 10}.
Prin urmare, relația R este tranzitivă pe mulțimea I.
Notă: Relațiile tranzitive se reprezintă frecvent prin grafuri. În asemenea reprezentări, tranzitivitatea poate fi observată cu ușurință urmărind conexiunile dintre noduri (elementele mulțimii). De exemplu, dacă există o săgeată de la 2 la 4 și alta de la 4 la 6, atunci trebuie să existe și o săgeată directă de la 2 la 6.
În schimb, tabelele cu dublă intrare și diagramele carteziene nu permit identificarea acestei proprietăți la fel de clar.
Alte exemple
- Relația "x este perpendiculară pe y" NU este tranzitivă. Dacă dreapta x formează un unghi de 90° cu dreapta y, iar aceasta formează la rândul ei un unghi de 90° cu dreapta z, atunci x și z formează un unghi de 180° (o linie dreaptă) sau de 0° (coincidente). În ambele cazuri, x și z nu sunt perpendiculare.