Relații Definite pe o Mulțime

O relație se spune că este definită pe o mulțime atunci când leagă elemente dintr-o mulțime A de alte elemente aparținând aceleiași mulțimi A.

Într-un asemenea caz, domeniul și codomeniul coincid.

Așadar, orice relație definită pe o mulțime reprezintă o submulțime a produsului cartezian A × A.

Un Exemplu Practic

Considerăm mulțimea finită A:

$$ A = \{ 2,3,4,5,6,7,8,9 \} $$

Produsul cartezian al lui A cu ea însăși, adică A × A, se notează astfel:

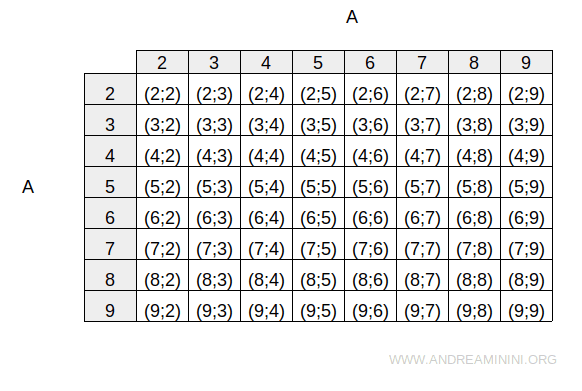
Definim o relație R pe A care asociază fiecărui element multiplii săi:

$$ R = \{ (2;2) , (2;4),(2;6),(2;8),(3;3),(3;6),(3;9)\\ \ \ \ \ \ \ \ \ \ \ \ \ (4;4) , (4;8),(5;5),(6;6),(7;7),(8;8),(9;9) \} $$

Această relație constituie, prin urmare, o submulțime a produsului cartezian A × A.

Reprezentarea sa sub formă de tabel cu dublă intrare este următoarea:

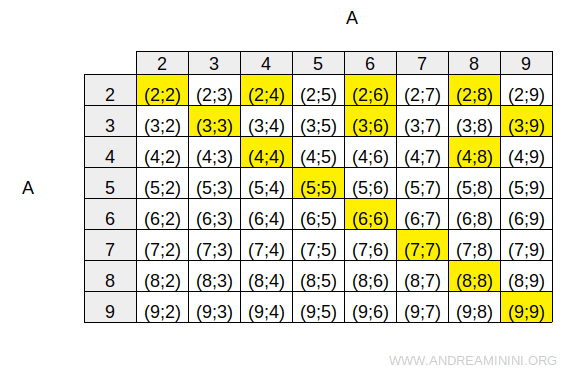
Diagrama cu săgeți (sau diagrama de corespondență) a acestei relații este:

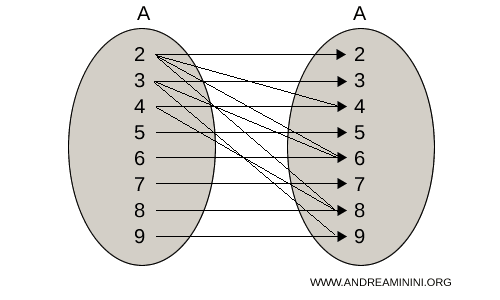
În acest exemplu, mulțimea A are simultan rolul de domeniu și de codomeniu.

Diagrama carteziană corespunzătoare se prezintă astfel:

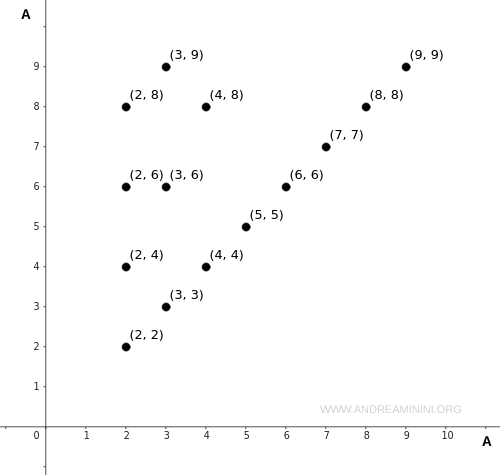
Se observă că mulțimea A apare pe ambele axe: axa orizontală (x) și axa verticală (y).

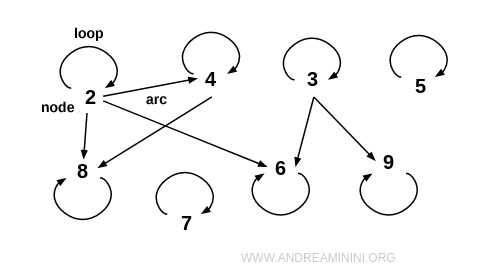
Notă. Relațiile definite pe o mulțime pot fi ilustrate și mai intuitiv printr-un graf. Fiecare element al lui A se reprezintă ca un nod, iar între nodurile corespunzătoare se trasează arce orientate. Atunci când un element este în relație cu el însuși - de pildă (2;2) - apare un arc special, numit buclă. În general, reprezentările grafice sunt mai clare, mai compacte și mai expresive vizual.

Tipuri de Relații Definite pe o Mulțime

Dintre relațiile care pot fi definite pe o mulțime, se disting câteva categorii esențiale:

• Relație Reflexivă
  O relație R pe mulțimea A este reflexivă dacă fiecare element a ∈ A este în relație cu el însuși. $$ \forall \ a \in A \Rightarrow \ aRa $$
• Relație Irreflexivă
  Relația R este irreflexivă dacă niciun element a ∈ A nu este în relație cu el însuși. $$ \forall \ a \in A \Rightarrow a \require{cancel} \cancel{R} a $$
• Relație Simetrică
  R este simetrică dacă, pentru orice a și b din A, faptul că a este în relație cu b implică și că b este în relație cu a. $$ aRb \ \Leftrightarrow \ bRa $$
• Relație Asimetrică
  R este asimetrică dacă, pentru orice a și b din A, dacă a este în relație cu b, atunci b nu este în relație cu a. $$ aRb \Rightarrow b \require{cancel} \cancel{R} a $$
• Relație Antisimetrică
  R este antisimetrică dacă, pentru toate a,b ∈ A cu a ≠ b, din faptul că a este în relație cu b rezultă că b nu este în relație cu a. $$ aRb , \ a \ne b \Rightarrow b \require{cancel} \cancel{R} a $$

  Care este diferența dintre asimetrică și antisimetrică? O relație antisimetrică permite reciprocitatea doar atunci când elementele coincid. Cu alte cuvinte, dacă a este în relație cu b și b cu a, atunci rezultă neapărat că a = b. $$ aRb , \ a \ne b \Rightarrow b \require{cancel} \cancel{R} a $$ În schimb, o relație asimetrică exclude orice reciprocitate, chiar și între elemente identice. $$ aRb \Rightarrow b \require{cancel} \cancel{R} a $$ În concluzie, asimetria interzice complet relațiile reciproce, pe când antisimetricitatea le acceptă numai atunci când elementele sunt identice.

• Relație Tranzitivă
  O relație R pe mulțimea A este tranzitivă dacă, ori de câte ori a este în relație cu b și b cu c, atunci și a este în relație cu c. $$ aRb , \ bRc \Rightarrow aRc $$

Și așa mai departe.