Relații de ordine

Relațiile de ordine sunt relații matematice care respectă trei proprietăți esențiale: reflexivitate, antisimetricitate și tranzitivitate.

• Reflexivitate: $$ \forall \ a \in A \:\: a\rho a $$
• Antisimetricitate: $$ \forall \ a,b \in A \ , \ a\rho b , \ a \ne b \Rightarrow b \require{cancel} \cancel{\rho} a $$
• Tranzitivitate: $$ \forall \ a,b,c \in A :\: [ a\rho b \land b\rho c ] \rightarrow a\rho c $$

Acest tip de relație se mai numește și ordine nestrictă.

Un concept înrudit este cel de ordine strictă, unde reflexivitatea este înlocuită de ireflexivitate.

În general, o relație este considerată de ordine dacă este reflexivă (sau ireflexivă), antisimetrică și tranzitivă.

Exemplu practic

Să luăm în considerare mulțimea numerelor naturale:

$$ N = \{ 1, 2, 3, 4, ... \} $$

Vrem să verificăm dacă relația R: "x este multiplu de y" definește o relație de ordine.

Analizăm pe rând cele trei proprietăți fundamentale:

• Reflexivitate: Orice număr este multiplu de sine însuși (de pildă, x = 1·x).
• Antisimetricitate: Dacă x și y sunt diferite, iar x este multiplu de y, atunci y nu poate fi multiplu de x.
• Tranzitivitate: Dacă x este multiplu de y și y este multiplu de z, atunci x este multiplu de z.

Deoarece toate condițiile sunt îndeplinite, R este într-adevăr o relație de ordine.

Ordine stricte și nestricte

Relațiile de ordine se împart în două mari categorii:

• Ordine nestrictă
  Acestea satisfac reflexivitatea, antisimetricitatea și tranzitivitatea.

  Exemplu: Relația "x este multiplu de y" este o ordine nestrictă. Este reflexivă (fiecare număr este multiplu de sine însuși, ca în 2·1=2 sau 3·1=3) și, în plus, respectă antisimetricitatea și tranzitivitatea.

• Ordine strictă
  Acestea respectă ireflexivitatea, antisimetricitatea și tranzitivitatea.

  Exemplu: Relația "x este mai înalt decât y" este o ordine strictă. Este ireflexivă (nimeni nu poate fi mai înalt decât sine) și respectă, de asemenea, antisimetricitatea și tranzitivitatea.

În concluzie, ordinele stricte sunt ireflexive, iar ordinele nestricte sunt reflexive.

Ordine parțiale și totale

Ordinele, fie stricte, fie nestricte, se clasifică și după gradul de comparabilitate dintre elemente. O relație de ordine poate fi parțială sau totală:

• Ordine parțială

  O ordine parțială compară doar anumite perechi de elemente, ceea ce înseamnă că nu toate elementele mulțimii pot fi puse în relație între ele.

  Se definește pe o submulțime a produsului cartezian. În acest context, mulțimea se numește mulțime parțial ordonată, deoarece numai unele perechi de elemente sunt comparabile.

  Exemplu: Mulțimea puterilor P(X), cu X = {1, 2, 3}, conține submulțimile {∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}. Sub relația de incluziune ⊆, se formează o ordine parțială: de pildă, {1} ⊆ {1,2}, în timp ce {3} nu este inclus în {1,2}. Structura se reprezintă astfel:
  

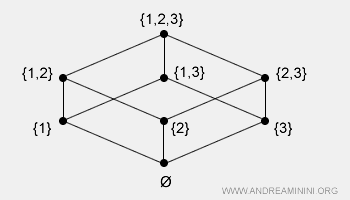
• Ordine totală

  O ordine totală permite compararea oricărei perechi de elemente: toate elementele sunt comparabile între ele.

  Se aplică tuturor perechilor (a, b) din mulțime. În acest caz, mulțimea se numește mulțime total ordonată sau lanț, datorită structurii sale liniare: orice două elemente pot fi comparate.

  Exemplu: Mulțimea X = {1, 2, 3} poate fi ordonată total prin relația ≤ (sau ≥). În acest caz, toate perechile de elemente sunt comparabile: 1ρ2, 2ρ3, 1ρ3 etc. Diagrama asociată formează un lanț, deoarece fiecare element este direct comparat cu celelalte.
  

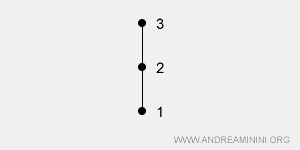
Reprezentarea grafică a relațiilor de ordine

Relațiile de ordine pe o mulțime X pot fi reprezentate grafic prin diagrame cu puncte unite prin segmente.

Fiecare punct reprezintă un element al mulțimii.

Un segment unește două elemente atunci când acestea sunt direct comparabile conform relației, adică atunci când între ele nu există niciun element intermediar.

Exemplu: În relația ≤, elementele 1 și 3 sunt comparabile. Totuși, pentru că între ele se află elementul 2, nu se trasează o legătură directă. În schimb, 1 și 2 sunt unite printr-un segment, la fel ca 2 și 3, deoarece între ele nu există elemente intermediare.

Mulțimi ordonate izomorfe

Două mulțimi ordonate sunt izomorfe dacă au aceeași structură relațională între elementele lor.

De exemplu, orice două mulțimi total ordonate cu aceeași cardinalitate vor fi întotdeauna izomorfe.

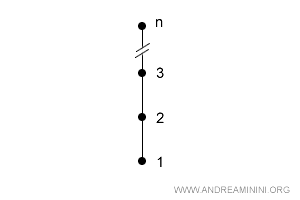
Prin urmare, mulțimile izomorfe împărtășesc aceeași structură de ordine, chiar dacă elementele lor sunt diferite.

Și așa mai departe.