Einfach zusammenhängende Räume in der Topologie
Ein topologischer Raum heißt einfach zusammenhängend, wenn sich jede geschlossene Kurve innerhalb des Raumes stetig zu einem einzigen Punkt zusammenziehen lässt.
Mit anderen Worten: Ein Raum ist genau dann einfach zusammenhängend, wenn sich jede Schleife in ihm zu einem Punkt kontrahieren lässt, ohne den Raum zu verlassen.
Das bedeutet, der Raum bildet ein zusammenhängendes „Ganzes“ ohne innere „Löcher“.
Hinweis: Jeder einfach zusammenhängende Raum ist automatisch auch zusammenhängend. Die Umkehrung gilt jedoch nicht: Nicht jeder zusammenhängende Raum ist zugleich einfach zusammenhängend.
Ein anschauliches Beispiel
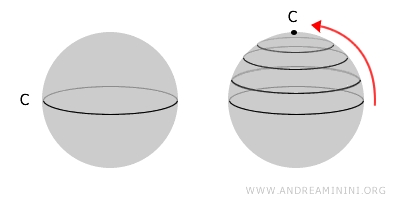
Eine Kugel ist ein typisches Beispiel für einen einfach zusammenhängenden Raum: Jede geschlossene Kurve auf oder in ihr kann stetig auf einen Punkt verkleinert werden.
Ein Torus oder „Donut“ dagegen ist nicht einfach zusammenhängend. Sein zentrales Loch verhindert, dass sich bestimmte Schleifen auf einen Punkt reduzieren lassen.
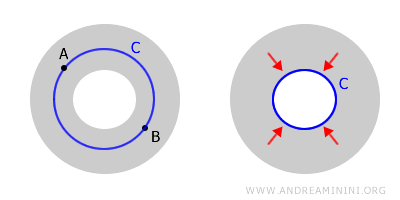
Damit wird klar: Zusammenhängend zu sein bedeutet nicht automatisch auch einfach zusammenhängend zu sein.
Der „Donut“ ist zwar zusammenhängend - denn zwei beliebige Punkte A und B lassen sich durch einen Weg innerhalb des Raumes verbinden -,
doch er ist nicht einfach zusammenhängend, da sich nicht jede geschlossene Kurve in ihm zu einem Punkt kontrahieren lässt.
In solchen Fällen, in denen ein Raum zwar zusammenhängend, aber nicht einfach zusammenhängend ist, spricht man von einem mehrfach zusammenhängenden Raum. Typische Beispiele sind der Ringbereich oder der Torus.
Damit gilt: Einfache Zusammenhang ist eine strengere Bedingung als Wegzusammenhang.
Und so weiter.