Zusammenhang bei nichtleerer Schnittmenge
Seien \( C_1, C_2, \dots, C_n \subset X \) zusammenhängende Teilmengen eines topologischen Raums \( X \), deren Schnittmenge nicht leer ist: \[
\bigcap_{i=1}^n C_i \neq \varnothing . \] Dann ist auch ihre Vereinigung \( \bigcup_{i=1}^n C_i \) zusammenhängend.
Anschaulich bedeutet das: Sobald mehrere zusammenhängende Mengen mindestens einen gemeinsamen Punkt besitzen, verschmelzen sie zu einer einzigen zusammenhängenden Struktur.
Der zentrale Gedanke ist einfach, aber grundlegend. Ein gemeinsamer Punkt verhindert, dass sich die Gesamtmenge in zwei voneinander getrennte, offene Teile aufspalten lässt. Genau darin liegt der Kern der Zusammenhangseigenschaft.
Bemerkung. Die Bedingung \( \bigcap_{i=1}^n C_i \neq \varnothing \) ist hinreichend, aber nicht notwendig. Auch ohne einen gemeinsamen Punkt kann eine Vereinigung zusammenhängend bleiben. Das ist insbesondere dann der Fall, wenn sich die Mengen überlappen oder kettenartig aneinander anschließen.
Ein anschauliches Beispiel
Betrachten wir drei Teilmengen der Ebene \( \mathbb{R}^2 \):
- \( C_1 \): das horizontale Streckenstück von \( (-1,0) \) bis \( (1,0) \)
- \( C_2 \): das vertikale Streckenstück von \( (0,-1) \) bis \( (0,1) \)
- \( C_3 \): das diagonale Streckenstück von \( (-1,-1) \) bis \( (1,1) \)
Jede dieser Mengen ist für sich genommen zusammenhängend.
Alle drei besitzen jedoch einen gemeinsamen Punkt, nämlich \( (0,0) \). Damit gilt:
\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]
Die gemeinsame Schnittmenge ist also nicht leer:
\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]
Nach dem oben formulierten Kriterium folgt daraus unmittelbar, dass auch ihre Vereinigung zusammenhängend ist:
\[ C_1 \cup C_2 \cup C_3 \]
Alle drei Strecken treffen sich in einem gemeinsamen Mittelpunkt. Genau dieser gemeinsame Punkt sorgt dafür, dass man innerhalb der Vereinigung von jeder Stelle aus jede andere erreichen kann.
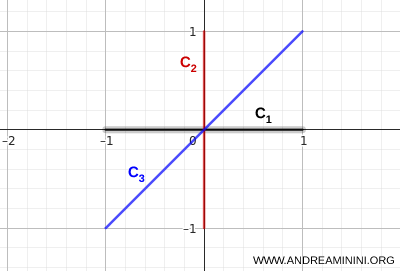
Man kann sich also entlang der Strecken bewegen, ohne jemals den zusammenhängenden Bereich zu verlassen.
Bemerkung. Es gibt weitere Kriterien für Zusammenhang, die nicht auf einem gemeinsamen Punkt aller Mengen beruhen. Sind die Mengen \( C_i \) zusammenhängend und überlappen sie sich kettenartig, also \( C_i \cap C_{i+1} \neq \varnothing \), dann ist auch ihre Vereinigung \( \bigcup_i C_i \) zusammenhängend, selbst wenn \( \bigcap_i C_i = \varnothing \) gilt. Diese Voraussetzung ist jedoch nicht zwingend. Auch dann, wenn einzelne aufeinanderfolgende Mengen disjunkt sind, kann die Gesamtmenge zusammenhängend bleiben, sofern andere Mengen die Verbindung herstellen. Ein klassisches Beispiel sind drei Strecken, die gemeinsam ein Dreieck bilden. Obwohl ihre gemeinsame Schnittmenge leer ist, also \( \bigcap_i C_i = \varnothing \), bleibt ihre Vereinigung zusammenhängend.
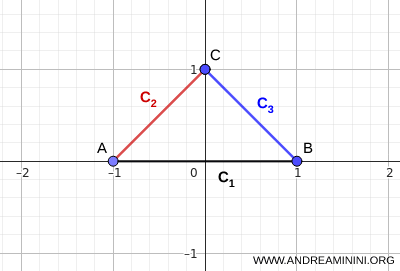
Dieses Beispiel zeigt anschaulich, dass Zusammenhang auch durch eine Kette lokaler Überlappungen entstehen kann.
Beweis
Sei \( X \) ein topologischer Raum und \( \{C_i\}_{i \in I} \) eine Familie zusammenhängender Teilmengen von \( X \), deren Schnittmenge nicht leer ist:
\[ \bigcap_{i \in I} C_i \neq \varnothing \]
Angenommen, die Vereinigung
\[ C = \bigcup_{i \in I} C_i \]
sei nicht zusammenhängend.
Dann existieren zwei offene Mengen \( U \) und \( V \), die eine Trennung von \( C \) bilden. Das bedeutet:
- \( U \cap C \neq \varnothing \)
- \( V \cap C \neq \varnothing \)
- \( (U \cap C) \cap (V \cap C) = \varnothing \)
- \( C = (U \cap C) \cup (V \cap C) \)
Da die Schnittmenge der Mengen \( C_i \) nicht leer ist, existiert ein Punkt
\[ x \in \bigcap_{i \in I} C_i \]
Dieser Punkt gehört zu allen Mengen \( C_i \) und damit insbesondere zu \( C \). Er liegt also entweder in \( U \) oder in \( V \), jedoch nicht in beiden, da diese eine Trennung von \( C \) bilden. Ohne Einschränkung der Allgemeinheit sei
\[ x \in U \quad \text{und} \quad x \notin V \]
Da jede Menge \( C_i \) in \( C \) enthalten ist, gilt:
\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]
Die Mengen \( C_i \cap U \) und \( C_i \cap V \) sind offen in der von \( C_i \) induzierten Teilraumtopologie, disjunkt und ihre Vereinigung ergibt wieder \( C_i \). Da jedes \( C_i \) zusammenhängend ist, muss eine dieser beiden Mengen leer sein.
Folglich ist jedes \( C_i \) vollständig entweder in \( U \) oder in \( V \) enthalten.
Da jedoch \( x \in C_i \) und zugleich \( x \in U \) gilt, kann kein \( C_i \) vollständig in \( V \) liegen. Somit folgt:
\[ C_i \subset U \quad \text{für alle } i \in I \]
Daraus ergibt sich, dass auch die gesamte Vereinigung in \( U \) enthalten ist:
\[ \bigcup_{i \in I} C_i \subset U \]
Dies steht im Widerspruch zur Annahme, dass \( V \cap C \neq \varnothing \) ist.
Der Widerspruch zeigt, dass die ursprüngliche Annahme falsch war. Somit ist die Vereinigung \( \bigcup_{i \in I} C_i \) eine zusammenhängende Menge.
Damit ist die Aussage bewiesen.