Jede zusammenhängende Teilmenge liegt in einer Zusammenhangskomponente des Raumes

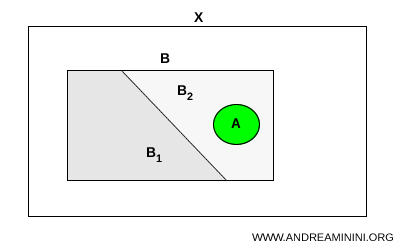
Seien $ A $ und $ B $ zwei Teilmengen eines topologischen Raumes $ X $. Wir nehmen an, dass $ A $ zusammenhängend ist und dass $ A \subset B $ gilt. Kann die Menge $ B $ im Raum $ X $ in zwei Teilmengen $ B_1 $ und $ B_2 $ zerlegt werden, so muss $ A $ vollständig in genau einer dieser beiden Teilmengen liegen: $$ A \subset B_1 \quad \text{oder} \quad A \subset B_2 $$

Anschaulich formuliert bedeutet dies: Eine zusammenhängende Teilmenge kann nicht gleichzeitig beide Teile einer Zerlegung berühren.

Sobald eine zusammenhängende Teilmenge in einer Menge liegt, die sich in zwei disjunkte Teile aufspalten lässt, ist eine Verteilung auf beide ausgeschlossen. Die Teilmenge bleibt vollständig innerhalb eines einzigen dieser Teile.

zusammenhängende Teilmenge, die vollständig innerhalb einer einzigen Zusammenhangskomponente einer topologischen Zerlegung liegt

Eine intuitive Vorstellung hilft beim Verständnis. Man kann sich eine zusammenhängende Teilmenge wie ein durchgehendes Seil vorstellen, das in einer Hülle liegt. Wird diese Hülle in zwei voneinander getrennte Fächer unterteilt, während das Seil unversehrt bleibt, so kann es sich nur in einem der beiden Fächer befinden. Um beide zu erreichen, müsste das Seil zerrissen werden. Genau diese Unmöglichkeit, eine Zerlegung zu überschreiten, beschreibt der Begriff der Zusammenhängigkeit.

Ein konkretes Beispiel
Beweis

Ein konkretes Beispiel

Betrachten wir den topologischen Raum:

$$ X = \mathbb{R} $$

und die folgende Teilmenge von $ X $:

$$ B = (-3,4) $$

Diese Menge lässt sich auf natürliche Weise in zwei Teilmengen zerlegen:

$$ B_1 = (-3,0) $$

$$ B_2 = (0,4) $$

Die beiden Teilmengen sind disjunkt:

$$ B_1 \cap B_2 = \varnothing $$

und ihre Vereinigung ergibt wieder die ursprüngliche Menge:

$$ B_1 \cup B_2 = B $$

Beide Mengen sind offen in der auf $ B $ induzierten Teilraumtopologie.

Damit bilden $ B_1 $ und $ B_2 $ eine Zerlegung von $ B $ im Raum $ X $.

Betrachten wir nun eine zusammenhängende Teilmenge von $ B $:

$$ A = (1,2) $$

Man erkennt sofort, dass $ A \subset B_2 $ gilt. Die Teilmenge $ A $ liegt also vollständig in einem der beiden Teile der Zerlegung, genau wie es das allgemeine Resultat vorhersagt.

Bemerkung. Wählt man hingegen $ A = (-1,1) $, so gilt $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ Eine solche Situation ist jedoch nicht zulässig, da $ B_1 $ und $ B_2 $ eine Zerlegung von $ B $ bilden. Eine zusammenhängende Teilmenge von $ B $ kann nicht auf beide Teile verteilt sein. Wäre dies möglich, so würde auch $ A $ selbst eine Zerlegung besitzen. Dies widerspricht der grundlegenden Tatsache, dass das Intervall $ (-1,1) $ zusammenhängend ist. Entscheidend ist daher nicht eine Veränderung der Zusammenhängigkeit von $ (-1,1) $, sondern die Unmöglichkeit, dass dieses Intervall in einer derart zerlegten Menge enthalten ist.

Beweis

Voraussetzungen

Seien $ A $ und $ B $ Teilmengen eines topologischen Raumes $ X $.

$$ A \subset X \quad \text{und} \quad B \subset X $$

Es gelte:

$ A $ ist zusammenhängend
$ A \subset B $
$ B_1 $ und $ B_2 $ bilden eine Zerlegung von $ B $ im Raum $ X $

Aussage

Unter diesen Voraussetzungen ist die Teilmenge $ A $ entweder in $ B_1 $ oder in $ B_2 $ enthalten:

$$ A \subset B_1 \quad \text{oder} \quad A \subset B_2 $$

Beweis

Nach Annahme bilden $ B_1 $ und $ B_2 $ eine Zerlegung von $ B $ im Raum $ X $. Insbesondere gilt:

$ B_1 \cap B_2 = \varnothing $
$ B = B_1 \cup B_2 $
$ B_1 $ und $ B_2 $ sind offen in der auf $ B $ induzierten Teilraumtopologie

Angenommen, um einen Widerspruch herzuleiten, $ A $ sei weder vollständig in $ B_1 $ noch vollständig in $ B_2 $ enthalten. Dann gilt:

$$ A \cap B_1 \neq \varnothing \qquad \text{und} \qquad A \cap B_2 \neq \varnothing $$

Da $ A \subset B $ ist, folgt:

$$ A = A \cap B = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$

Die Mengen $ A \cap B_1 $ und $ A \cap B_2 $ sind disjunkt, da $ B_1 $ und $ B_2 $ disjunkt sind.

Da $ B_1 $ und $ B_2 $ offen in $ B $ sind, sind auch $ A \cap B_1 $ und $ A \cap B_2 $ offen in der auf $ A $ induzierten Teilraumtopologie.

Damit zerlegt sich $ A $ in zwei disjunkte, nichtleere und offene Teilmengen. Dies definiert eine Zerlegung von $ A $ im Raum $ X $.

Dies widerspricht der Annahme, dass $ A $ zusammenhängend ist.

Folglich ist die anfängliche Annahme falsch, und es gilt:

$$ A \subset B_1 \quad \text{oder} \quad A \subset B_2 $$

Damit ist die Aussage gezeigt.

Und so weiter.