Zusammenhang in der Topologie

In der Topologie heißt ein Raum zusammenhängend, wenn er sich nicht in zwei disjunkte offene Mengen zerlegen lässt. Mit anderen Worten: Zusammenhang bedeutet, dass sich beliebige zwei Punkte des Raums durch einen Pfad verbinden lassen, ohne den Raum zu verlassen.

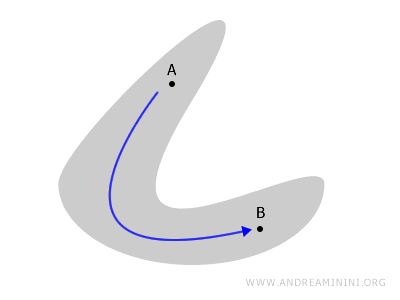
Zusammenhang beschreibt also, ob die Teile eines topologischen Raums miteinander verbunden oder voneinander getrennt sind.

Dieses Konzept ist - neben der Stetigkeit - eine Grundidee der Topologie.

Der Zusammenhang liefert in vielen Bereichen der Mathematik wesentliche Informationen über die innere Struktur eines Raums und das Verhältnis seiner Teilmengen. Er ist daher ein wichtiges Werkzeug bei Klassifikation und Analyse topologischer Räume.

Ein praktisches Beispiel

Eine Figur in der Ebene oder ein Polyeder ist zusammenhängend, wenn es einen stetigen Pfad gibt, der zwei beliebige Punkte A und B verbindet, ohne den Raum zu verlassen.

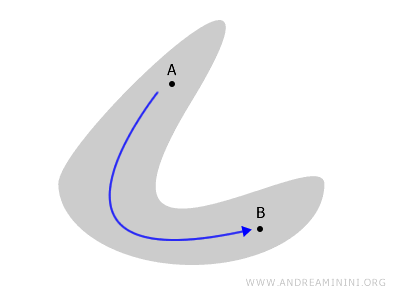
Sind dagegen Teile des Raums voneinander getrennt, so ist der Raum nicht zusammenhängend (disconnected space).

In diesem Fall zerfällt er in zwei disjunkte Bereiche. Jeder Pfad von A nach B müsste den Raum verlassen.

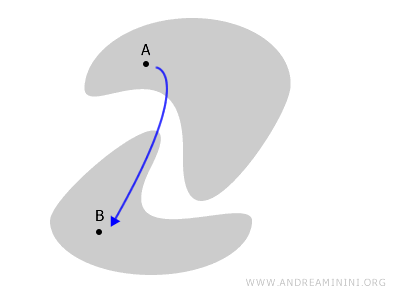
Wann ist ein Raum nicht zusammenhängend?

Ein anschauliches Beispiel sind zwei getrennte Zimmer in einem Gebäude, die durch eine Wand voneinander getrennt sind. Jedes Zimmer entspricht einer offenen Menge, die ihre Grenze (die Wand) nicht enthält, sodass beide Mengen disjunkt sind.

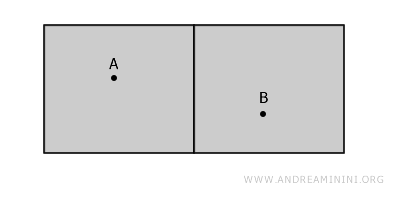
Obwohl die Zimmer nebeneinanderliegen, sind sie nicht verbunden, da jeder Weg von A nach B die Wand durchqueren müsste - ein Bereich, der nicht zum Raum gehört.

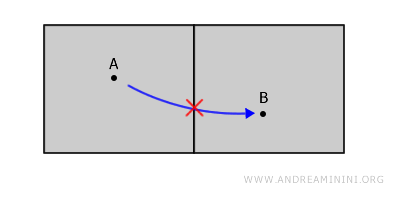
Wichtig ist daher: Ränder gehören nicht zu offenen Mengen.

Lokaler Zusammenhang

Ein Raum ist lokal zusammenhängend, wenn jede Umgebung eines Punktes einen zusammenhängenden Teilraum enthält. Das heißt: Jeder Punkt liegt in einer zusammenhängenden offenen Teilmenge.

Betrachten wir erneut das Beispiel zweier disjunkter Zimmer:

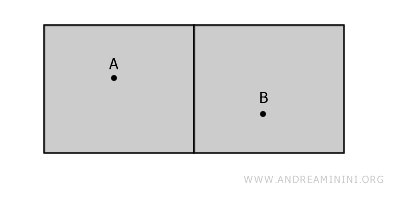
Global ist der Raum nicht zusammenhängend, da A und B nicht ohne Wanddurchquerung verbunden werden können.

An Punkt A jedoch existiert eine offene Umgebung, deren Punkte alle miteinander verbunden sind - ein Beispiel für lokalen Zusammenhang.

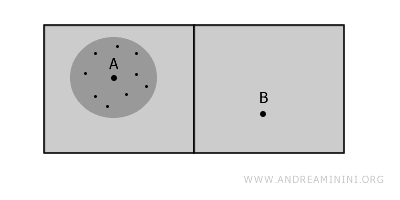
Dasselbe gilt für Punkt B.

Arten des Zusammenhangs

Von den verschiedenen Formen des Zusammenhangs sind zwei besonders wichtig:

• Topologischer Zusammenhang
  Ein topologischer Raum $ X $ heißt zusammenhängend, wenn er sich nicht in zwei offene, disjunkte und nichtleere Teilmengen zerlegen lässt, deren Vereinigung den gesamten Raum ergibt. Anders gesagt: Es gibt keine Möglichkeit, den Raum in zwei voneinander getrennte Bereiche zu teilen, die zugleich offen und nichtleer sind.

  Beispiel. Der Raum (-1, 1) ist zusammenhängend, während der Raum (-1, 0) ∪ (0, 1) nicht zusammenhängend ist. In diesem Fall existieren nämlich zwei offene, disjunkte und nichtleere Mengen - (-1, 0) und (0, 1) - deren Vereinigung den gesamten Raum bildet.
  Diese beiden Mengen stellen somit eine Trennung des Raums dar.

• Wegzusammenhang (oder Bogenzusammenhang)
  Ein topologischer Raum heißt wegzusammenhängend, wenn es für jedes Paar von Punkten A und B im Raum einen stetigen Weg gibt, der beide verbindet und vollständig innerhalb des Raums verläuft. Jeder wegzusammenhängende Raum ist auch zusammenhängend, doch gilt die Umkehrung nicht notwendigerweise.
  

  Betrachten wir beispielsweise eine geschlossene Figur in der Ebene. Für jedes Paar von inneren Punkten A und B lässt sich eine stetige Kurve zeichnen, die beide miteinander verbindet, ohne den Stift abzusetzen oder die Figur zu verlassen.
  
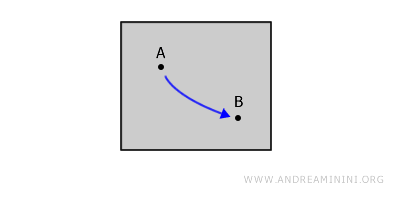
  Unterschied zwischen Bogen- und Wegzusammenhang.  Der Bogenzusammenhang ist dem Wegzusammenhang sehr ähnlich, jedoch muss der Weg in diesem Fall injektiv sein, das heißt, er darf sich nicht selbst schneiden und keinen Punkt mehr als einmal durchlaufen.

• Einfacher Zusammenhang
  Ein Raum ist einfach zusammenhängend, wenn sich jede geschlossene Kurve darin stetig auf einen Punkt zusammenziehen lässt. Solche Räume enthalten keine inneren „Löcher“. Jeder einfach zusammenhängende Raum ist zusammenhängend, aber nicht jeder zusammenhängende Raum ist einfach zusammenhängend. Formal: In einem einfach zusammenhängenden Raum ist jede Schleife homotop zu einem Punkt.
  

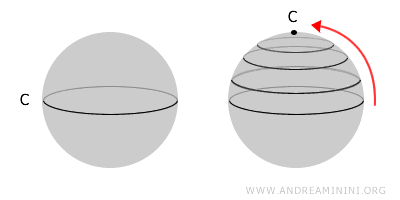
  Die Kugeloberfläche ist einfach zusammenhängend, da sich jede Schleife auf einen Punkt verkleinern lässt. Ein Torus dagegen besitzt ein Loch: Er ist zwar zusammenhängend, aber nicht einfach zusammenhängend.
  
  
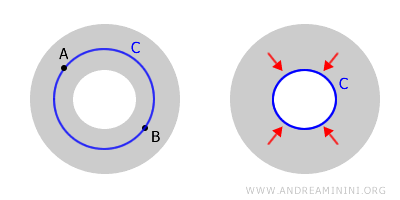
  Ein solcher Raum heißt mehrfach zusammenhängend. Ein Ringgebiet ist ein klassisches Beispiel.

Bemerkungen

• Im Raum der reellen Zahlen sind die einzigen zusammenhängenden Mengen Intervalle.