Topologie

Die Topologie ist ein Teilgebiet der Mathematik, das sich mit den grundlegenden Eigenschaften von Räumen beschäftigt, die unter stetigen Verformungen erhalten bleiben. Gemeint sind Veränderungen wie Dehnen, Biegen oder Verdrehen, solange ein Objekt weder zerrissen noch neu zusammengesetzt wird.

Aus dieser Perspektive richtet sich der Blick der Topologie auf jene geometrischen Eigenschaften, die stabil bleiben, solange die betrachteten Transformationen stetig sind.

Eine Veränderung dieser Eigenschaften ist nur durch unstetige Eingriffe möglich, etwa wenn ein Raum aufgeschnitten wird oder wenn zwei zuvor getrennte Bereiche künstlich miteinander verbunden werden.

Ein klassisches Beispiel liefern die Sphäre und der Würfel, die topologisch äquivalent sind, sofern man ihre Oberflächen betrachtet. Tatsächlich lässt sich die eine durch eine stetige Verformung in den anderen überführen, ohne schneiden oder kleben zu müssen.

Anders verhält es sich bei einer Sphäre und einem Torus. Diese sind nicht topologisch äquivalent, da der Übergang vom einen zum anderen das Erzeugen oder Entfernen eines Lochs erfordern würde. Ein solcher Schritt setzt zwangsläufig Schneide- oder Klebeoperationen voraus.

Vereinfacht gesagt interessiert sich die Topologie weniger für exakte Maße wie Abstände, Größen oder konkrete Formen, sondern vielmehr dafür, wie Räume aufgebaut sind und wie ihre Teile miteinander zusammenhängen.

Begriffe wie Länge, Fläche, Volumen oder Winkelmaß treten dabei in den Hintergrund. Im Vordergrund stehen stattdessen die qualitativen Eigenschaften geometrischer Objekte und die Frage, ob und wie sie durch stetige Verformungen ineinander überführt werden können.

Zu den zentralen Themen dieses Ansatzes gehören unter anderem der Zusammenhang, die Kompaktheit, die Anzahl der Löcher eines Objekts sowie weitere globale Eigenschaften eines Raums.

Ein grundlegender Begriff der Topologie ist der des topologischen Raums. Die maßgeblichen Abbildungen in diesem Kontext sind die Homöomorphismen. Dabei handelt es sich um stetige, bijektive Abbildungen, deren Umkehrabbildung ebenfalls stetig ist. Sie erlauben es, einen Raum zu verändern, ohne seine topologische Struktur zu verlieren.

Aus diesem Grund wird die Topologie häufig als „Gummituchgeometrie“ bezeichnet. Man stellt sich geometrische Objekte als aus einem elastischen Material bestehend vor, das man dehnen, biegen oder zusammendrücken kann, jedoch weder zerreißen noch neu zusammenkleben darf. In dieser anschaulichen Form gehört die Topologie heute zu den grundlegenden und stark vereinheitlichenden Disziplinen der modernen Mathematik.

Geschichte

Ihren Ursprung hat die Topologie im 18. Jahrhundert.

Sie geht zurück auf Leonhard Eulers berühmtes Problem der sieben Brücken von Königsberg, das grundlegende Ideen wie Zusammenhang und Netzwerkanalyse einführte.

Aus dieser Fragestellung ergaben sich erstmals grundlegende Überlegungen zu den Eigenschaften von Räumen - und damit die Basis der Topologie.

Das Brückenproblem: Auf einer Flussinsel befinden sich sieben Brücken. Von einem beliebigen Startpunkt aus soll jede Brücke genau einmal überquert werden - ohne eine Brücke zweimal zu benutzen.

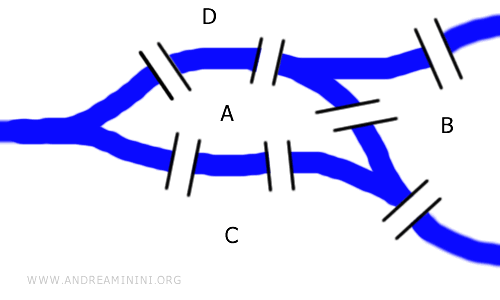
Für die Lösung sind weder Entfernungen noch Brückenlängen relevant. Es handelt sich um ein genuin topologisches Problem, das man mit Graphen darstellen kann. Der hier gezeigte Graph ist topologisch äquivalent zur ursprünglichen Brückenanordnung.

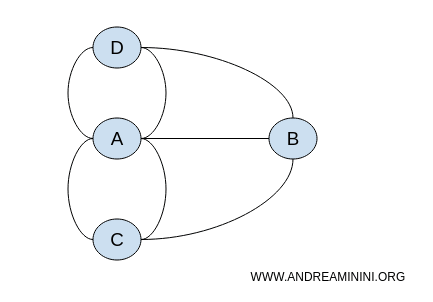
Die konkrete Lage der Knoten ist dabei unwichtig. Entscheidend sind allein die Verbindungen zwischen ihnen. Deshalb lässt sich das Problem in unendlich vielen verschiedenen, aber topologisch gleichwertigen Graphen darstellen.

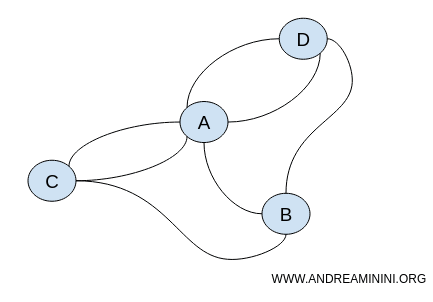
Beide Graphen bewahren dieselben topologischen Eigenschaften wie Stetigkeit und Zusammenhang.

Euler erkannte, dass das Brückenproblem zwar geometrisch anmutet, jedoch nicht auf Messungen beruht.

Er zeigte, dass es im Kern eine Frage der Lagebeziehungen ist, und bewies, dass es unlösbar ist. Damit begründete er die "Geometrie der Lage".

Im 19. Jahrhundert vertieften Mathematiker wie Carl Friedrich Gauß, August Ferdinand Möbius, Johann Listing, Bernhard Riemann und Felix Klein die Untersuchung von Flächen und Formen und prägten das Verständnis topologischer Eigenschaften.

Hinweis: Johann Listing prägte 1847 den Begriff "Topologie", der sich jedoch erst Jahrzehnte später in der Fachwelt etablierte.

Die Geometrie der Lage fand im 19. Jahrhundert praktische Anwendung, etwa in Gustav Kirchhoffs Netzwerktheorie.

Henri Poincaré schließlich lieferte Ende des 19. und Anfang des 20. Jahrhunderts mit der algebraischen Topologie zentrale Beiträge.

Im 20. Jahrhundert differenzierte sich die Topologie in spezialisierte Bereiche wie algebraische Topologie und allgemeine Topologie, geprägt von Mathematikern wie Felix Hausdorff, Georg Cantor und Luitzen Brouwer - insbesondere im Bereich der abstrakten Mathematik.

Heute ist die Topologie ein zentrales Gebiet der Mathematik, das sich den Eigenschaften widmet, die unter stetigen Verformungen unverändert bleiben.

Sie umfasst zahlreiche Teilgebiete: algebraische, differentielle, allgemeine und geometrische Topologie.

Insgesamt lässt sich die Topologie sowohl als allgemeine Lehre der Formen verstehen als auch als hochabstrakte mathematische Disziplin.

Trotz ihrer Abstraktheit haben topologische Konzepte vielfältige Anwendungen - von der Ökonomie über die Ingenieurwissenschaften bis hin zu den Naturwissenschaften.

Topologische Räume

Ein topologischer Raum ist eine Menge X mit einer Struktur T, der sogenannten "Topologie". Sie liefert den Rahmen, um Begriffe wie Stetigkeit, Nähe oder Grenzwerte weit allgemeiner zu erfassen, als es in der klassischen Geometrie oder Analysis möglich ist.

$$ (X,T) $$

Beispiel: Ein klassisches Beispiel ist die reelle Zahlenachse \( \mathbb{R} \) mit der Standardtopologie. Eine Menge ist offen, wenn sie um jeden Punkt ein Intervall enthält. Damit lassen sich Stetigkeit und Grenzwerte topologisch beschreiben.

Homöomorphismen

Ein Homöomorphismus ist eine bijektive stetige Abbildung zwischen zwei topologischen Räumen, deren Umkehrabbildung ebenfalls stetig ist. Damit bleiben alle wesentlichen topologischen Eigenschaften erhalten.

Zwei Räume gelten in der Topologie als "wesentlich gleich", wenn sie durch einen Homöomorphismus ineinander überführbar sind.

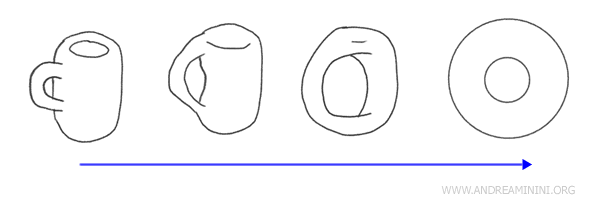
Beispiel: Das Verformen einer Kaffeetasse zu einem Donut ist das klassische Beispiel: Beide Objekte besitzen genau ein Loch und lassen sich durch stetige Verformungen ineinander überführen, ohne Schneiden oder Kleben - ihre grundlegenden topologischen Eigenschaften bleiben bestehen.

Geometrie versus Topologie

Geometrie und Topologie sind unterschiedliche Disziplinen, greifen aber eng ineinander, da sie verschiedene Aspekte mathematischer Räume beleuchten.

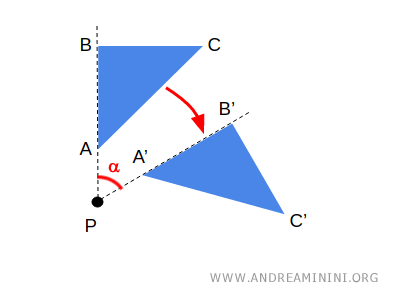
• Geometrie untersucht Eigenschaften wie Abstände, Winkel und Maße und konzentriert sich auf konkrete Figuren und deren räumliche Beziehungen. Ein Beispiel ist die Drehung einer Figur - eine geometrische Transformation, die Längen erhält.
  

  Die euklidische Geometrie ist die vertrauteste Form. In nichteuklidischen Geometrien hingegen werden die Konsequenzen betrachtet, wenn man das Parallelenaxiom Euklids lockert oder aufhebt.

• Topologie betrachtet Eigenschaften, die auch unter stetigen Verformungen wie Strecken oder Stauchen unverändert bleiben, solange nicht gerissen oder geklebt wird. Sie beschäftigt sich mit qualitativen Aspekten wie Zusammenhang, Stetigkeit und der Flexibilität von Formen. So bleibt beim Verformen eines Würfels zu einer Kugel die Verbindung der Punkte erhalten - ein Paradebeispiel für eine topologische Transformation.
  

  Beispiel: Ein Tonwürfel lässt sich zu einer Kugel formen, ohne Material hinzuzufügen oder wegzunehmen. Zusammenhang und Stetigkeit bleiben bestehen - ein anschaulicher Homöomorphismus, der Kern topologischer Transformationen.
  

Auch wenn sie unterschiedliche Schwerpunkte haben, sind Geometrie und Topologie eng verzahnt - oft gilt die Topologie als Verallgemeinerung der Geometrie.

Topologie erweitert den Blick auf abstraktere Eigenschaften von Räumen, während die Geometrie stärker an konkreten Messgrößen orientiert ist.

Zweige der Topologie

Die Topologie ist vielseitig anwendbar, und ihre Teilgebiete setzen jeweils unterschiedliche Schwerpunkte.

• Geometrische Topologie: Sie untersucht Eigenschaften, die unter Transformationen wie Strecken, Stauchen oder Falten erhalten bleiben, solange nicht gerissen oder geklebt wird. Wichtige Themen sind Zusammenhang, Kompaktheit oder Ränder - unabhängig von Distanzen.
• Allgemeine Topologie (Mengenlehre-Topologie): Sie betrachtet topologische Räume abstrakt und untersucht offene und abgeschlossene Mengen, Stetigkeit, Kompaktheit, Zusammenhang sowie metrische und Funktionenräume.
• Algebraische Topologie: Hier werden algebraische Methoden eingesetzt, um topologische Räume zu analysieren. Dadurch lassen sich ihre Strukturen und Eigenschaften tiefer verstehen.
• Differentialtopologie: Sie verwendet Techniken der Analysis, um topologische Räume zu studieren, die lokal wie der euklidische Raum aussehen. So lassen sich Begriffe wie Tangentialität oder Differenzierbarkeit präzise fassen.
• Angewandte Topologie: Sie widmet sich der Nutzung topologischer Methoden in praktischen Kontexten, etwa in der Datenanalyse, Netzwerkwissenschaft, Technik oder Biologie.

Jeder dieser Bereiche hat eigene Methoden und Fragestellungen - zusammen zeigen sie die Breite und Relevanz topologischer Konzepte.