Häufungspunkte in der Topologie

In einem topologischen Raum $X$ bezeichnet man einen Punkt $x$ als Häufungspunkt einer Teilmenge $A \subseteq X$, wenn jede Umgebung von $x$ mindestens einen Punkt aus $A$ enthält, der von $x$ verschieden ist.

Anschaulich bedeutet das: Ganz gleich, wie klein man die Umgebung von $x$ wählt, man findet darin immer wieder Punkte aus $A$, die nicht mit $x$ selbst zusammenfallen.

Formal lässt sich diese Eigenschaft so ausdrücken: Für jede Umgebung $U$ von $x$ ist der Schnitt mit $A$ nicht leer.

$$ U \cap A \neq \emptyset $$

Wichtig ist dabei, dass ein Häufungspunkt nicht notwendigerweise zur Menge $A$ gehören muss. Er kann auch außerhalb der betrachteten Teilmenge liegen.

Im topologischen Raum der reellen Zahlen $\mathbb{R}$ ist der Begriff des Häufungspunktes besonders leicht zugänglich. Auf der reellen Zahlengeraden ist ein Punkt $x$ genau dann ein Häufungspunkt einer Teilmenge $A$, wenn jede Umgebung von $x$, also jedes offene Intervall der Form $(x-\epsilon, x+\epsilon)$, mindestens einen von $x$ verschiedenen Punkt aus $A$ enthält.
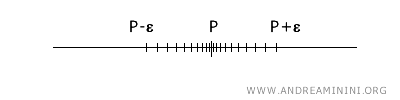
Anschauliche Darstellung eines Häufungspunktes auf der reellen Zahlengeraden
Die topologische Definition verallgemeinert dieses intuitive Bild auf den $n$-dimensionalen Raum $\mathbb{R}^n$. Auch dort ist ein Punkt $x$ ein Häufungspunkt einer Menge $A$, wenn jede Umgebung von $x$ einen Punkt aus $A$ enthält, der von $x$ verschieden ist. In höheren Dimensionen verliert diese Vorstellung jedoch oft etwas von ihrer Anschaulichkeit.

Konkrete Beispiele
Anmerkungen

Konkrete Beispiele

Betrachten wir zunächst eine einfache, aber sehr typische Situation in $\mathbb{R}$ mit der üblichen Topologie.

$$ A = \left\{ \frac{1}{n} \mid n \in \mathbb{N}^+ \right\} $$

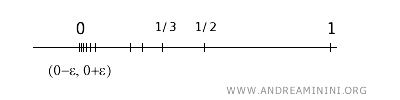
Diese Menge besteht aus den Punkten $ \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots $, also aus $\{1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \ldots \}$.

Um zu entscheiden, ob $0$ ein Häufungspunkt von $A$ ist, betrachten wir eine beliebige offene Umgebung von $0$.

Jede solche Umgebung enthält ein offenes Intervall $(a, b)$ mit $a < 0 < b$.

Da die Folge $\frac{1}{n}$ für $n \to \infty$ gegen $0$ konvergiert, liegt für hinreichend großes $n$ stets ein Wert $\frac{1}{n}$ innerhalb dieses Intervalls.

Damit enthält jede Umgebung von $0$ mindestens einen Punkt aus $A$, der von $0$ verschieden ist.

Folglich ist $0$ ein Häufungspunkt der Menge $A$.

Grafische Darstellung eines Häufungspunktes

Beispiel 2

Betrachten wir nun eine andere Menge in $\mathbb{R}$:

$$ B = \left\{ n + \frac{1}{n} \mid n \in \mathbb{N}^+ \right\} $$

Diese Menge enthält die Punkte $ 1 + 1, 2 + \frac{1}{2}, 3 + \frac{1}{3}, \ldots $, also näherungsweise $\{2, 2.5, 3.333\ldots, \ldots \}$.

Wir untersuchen, ob der Punkt $1$ ein Häufungspunkt von $B$ ist.

Jede offene Umgebung von $1$ enthält ein Intervall $(a, b)$ mit $a < 1 < b$.

Alle Elemente der Menge $B$ sind jedoch strikt größer als $1$. Damit ein Element von $B$ in einem solchen Intervall liegt, müsste der Ausdruck $n + \frac{1}{n}$ zwischen $a$ und $b$ liegen.

Da kein Element von $B$ kleiner oder gleich $1$ ist, enthält keine Umgebung von $1$ Punkte aus $B$.

Somit ist $1$ kein Häufungspunkt der Menge $B$.

Beispiel 3

Betrachten wir abschließend das Intervall $(0, 1]$ als Teilmenge von $\mathbb{R}$ mit der üblichen Topologie.

Ziel ist es, alle Häufungspunkte dieser Menge zu bestimmen.

Nach der Definition ist ein Punkt $x$ genau dann ein Häufungspunkt von $(0, 1]$, wenn jede Umgebung von $x$ das Intervall $(0, 1]$ in mindestens einem von $x$ verschiedenen Punkt schneidet.

Innere Punkte von $(0,1]$
Sei $x \in (0, 1]$. Jede Umgebung von $x$ enthält ein offenes Intervall $(a, b)$ mit $a < x < b$. Da $x$ zu $(0, 1]$ gehört, enthält diese Umgebung stets Punkte aus $(0, 1)$, die von $x$ verschieden sind. Jeder Punkt $x \in (0, 1]$ ist daher ein Häufungspunkt von $(0, 1]$.
Randpunkte von $(0,1]$
Betrachten wir nun die Randpunkte $0$ und $1$.
- Punkt $0$ : Obwohl $0$ nicht zur Menge $(0, 1]$ gehört, enthält jede Umgebung von $0$ ein Intervall $(a, b)$ mit $a < 0 < b$, das unendlich viele positive Punkte aus $(0, 1]$ enthält. Daher ist $0$ ein Häufungspunkt von $(0, 1]$.

- Punkt $1$ : Da $1$ selbst zu $(0, 1]$ gehört, enthält jede Umgebung von $1$, etwa ein offenes Intervall $(a, b)$ mit $a < 1 < b$, unendlich viele Punkte aus $(0, 1)$, die von $1$ verschieden sind. Auch $1$ ist somit ein Häufungspunkt von $(0, 1]$.
Punkte außerhalb von $[0, 1]$
Abschließend betrachten wir Punkte $x \notin [0, 1]$. Liegt $x < 0$ oder $x > 1$, so lässt sich immer eine Umgebung von $x$ finden, die vollständig disjunkt zu $(0, 1]$ ist.
Ist beispielsweise $x < 0$, kann man ein offenes Intervall $(x - \epsilon, x + \epsilon)$ mit hinreichend kleinem $\epsilon$ wählen, das keinen Punkt aus $(0, 1]$ enthält. Entsprechend existiert für $x > 1$ ein offenes, um $x$ zentriertes Intervall, das vollständig disjunkt zu $(0, 1]$ ist. Somit ist kein Punkt außerhalb des abgeschlossenen Intervalls $[0, 1]$ ein Häufungspunkt von $(0, 1]$.

Zusammenfassend zeigt dieses Beispiel, dass die Häufungspunkte des Intervalls $(0, 1]$ im topologischen Raum $\mathbb{R}$ mit der üblichen Topologie genau die Punkte des abgeschlossenen Intervalls $[0, 1]$ sind.

Beispiel 4

Untersuchen wir nun die Häufungspunkte der Teilmenge $ A = (0, 1] $ in der Topologie des unteren Randes auf $ \mathbb{R} $.

Die Topologie des unteren Randes auf $ \mathbb{R} $, häufig auch als Sorgenfrey-Topologie bezeichnet, wird durch Intervalle der Form $[a, b)$ mit $ a < b $ erzeugt. Die offenen Mengen dieser Topologie bestehen somit aus beliebigen Vereinigungen solcher halboffenen Intervalle.

Ein Punkt $x$ heißt Häufungspunkt einer Menge $A$, wenn jede Umgebung von $x$ mindestens einen Punkt aus $A$ enthält, der von $x$ verschieden ist.

Wir betrachten nun systematisch die möglichen Fälle.

Der Fall $x \in (0, 1)$
Jede Umgebung von $x$ enthält in dieser Topologie ein Intervall der Form $[x, x + \epsilon)$ und damit unendlich viele Punkte aus $A$. Jeder Punkt des offenen Intervalls $(0, 1)$ ist daher ein Häufungspunkt von $A$.
Der Fall $x = 1$
Zwar existieren in der Topologie des unteren Randes keine Umgebungen der Form $(1 - \epsilon, 1]$, dennoch gibt es Umgebungen von $1$ vom Typ $[1 - \epsilon, 1)$, die Punkte aus $A$ enthalten. Auch der Punkt $1$ ist somit ein Häufungspunkt von $A$.
Der Fall $x = 0$
Jede Umgebung von $0$, also jedes Intervall der Form $[0, \epsilon)$, schneidet die Menge $A$ in unendlich vielen Punkten. Damit ist auch $0$ ein Häufungspunkt von $A$.
Der Fall $x < 0$ oder $x > 1$
Für solche Punkte lässt sich stets eine Umgebung der Form $[x, x + \epsilon)$ finden, die keinen Punkt aus $A$ enthält. Punkte außerhalb des Intervalls $[0, 1]$ sind daher keine Häufungspunkte von $A$.

Zusammenfassend zeigt sich, dass die Häufungspunkte der Menge $ A = (0, 1] $ in der Topologie des unteren Randes auf $ \mathbb{R} $ genau mit den Punkten des abgeschlossenen Intervalls $[0, 1]$ übereinstimmen.

Die Menge aller Häufungspunkte von $ A $ ist also gleich $[0, 1]$.

Anmerkungen

Zum Abschluss einige weiterführende Hinweise, die den Zusammenhang zwischen Häufungspunkten und anderen grundlegenden Begriffen der Topologie verdeutlichen.

Abschluss und Häufungspunkte
Der Abschluss einer Teilmenge $A$ eines topologischen Raumes $X$ ergibt sich als Vereinigung von $A$ mit der Menge $A'$ ihrer Häufungspunkte: $$ \text{Cl}(A) = A \cup A' $$ Äquivalent dazu ist $\text{Cl}(A)$ die kleinste abgeschlossene Teilmenge von $X$, die $A$ enthält. Sie umfasst sowohl die Punkte von $A$ selbst als auch alle Grenzpunkte von Folgen, oder allgemeiner von Netzen oder Filtern, deren Elemente aus $A$ stammen.
Konvergenz in einem topologischen Raum
Ist $ A \subseteq \mathbb{R} $ mit der üblichen Topologie und ist $ x $ ein Häufungspunkt von $ A $, so existiert eine Folge $ \{x_i\} \subseteq A \setminus \{x\} $, die gegen $ x $ konvergiert. Der Grenzpunkt muss dabei nicht notwendigerweise selbst zur Menge $ A $ gehören.
Eindeutigkeit von Grenzwerten
In der üblichen Topologie auf $ \mathbb{R} $ ist der Grenzwert einer Folge eindeutig, sofern er existiert. Diese Eigenschaft gilt jedoch nicht in allen topologischen Räumen. In nicht hausdorffschen Räumen kann eine und dieselbe Folge gegen mehrere verschiedene Punkte konvergieren. Die Eindeutigkeit des Grenzwertes ist daher eng mit den Trennungseigenschaften des betrachteten Raumes verknüpft.

Diese Beobachtungen machen deutlich, welche zentrale Rolle Häufungspunkte für das Verständnis von Abschluss, Konvergenz und den grundlegenden Strukturen topologischer Räume spielen.