Die Basis einer Topologie

Die Basis einer Topologie ist eine Menge B offener Teilmengen, mit deren Hilfe sich jede offene Menge einer Topologie T als Vereinigung von Mengen aus B darstellen lässt.

Ausgangspunkt ist eine Menge X und eine Familie T von Teilmengen von X, die zusammen eine Topologie bilden. Eine Basis dieser Topologie ist eine Kollektion B von Mengen, den sogenannten Basiselementen, die zwei grundlegende Bedingungen erfüllen:

• Jedes Element x ∈ X liegt in mindestens einer Menge aus B.
• Wenn x im Schnitt zweier Basiselemente B₁ und B₂ liegt, dann gibt es ein weiteres Basiselement B₃ in B, das innerhalb dieses Schnitts liegt und ebenfalls x enthält.
  

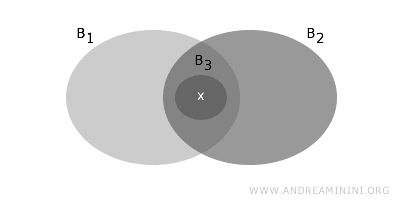
Erfüllt eine Kollektion diese beiden Bedingungen, so bildet sie eine Basis für die Topologie T.

Warum ist das wichtig?

Das Konzept der Basis ist ein zentrales Werkzeug in der Topologie. Es erlaubt, eine Topologie nicht durch alle ihre offenen Mengen zu beschreiben, sondern durch eine kleinere, leichter handhabbare Sammlung von „Grundbausteinen“. Aus diesen Bausteinen lassen sich dann alle offenen Mengen zusammensetzen.

Hinweis. Die Bedingung über die Schnitte offener Mengen stellt sicher, dass die Topologie ihre fundamentalen Eigenschaften erfüllt, insbesondere dass der Schnitt zweier offener Mengen ebenfalls offen ist.

Ein einfaches Beispiel

Betrachten wir die Menge:

$$ X = \{a, b, c \} $$

und die Topologie:

$$ T = \{ \emptyset, \{ a \}, \{ b,c \}, \{ a,b,c \} \} $$

Hier beschreibt T die Gesamtheit der offenen Mengen in X.

Eine mögliche Basis B dieser Topologie ist:

$$ B = \{ \{ a \}, \{ b,c \} \} $$

Diese Wahl erfüllt die beiden Bedingungen: Jedes Element von X liegt in mindestens einer Menge aus B, und jede offene Menge von T lässt sich als Vereinigung von Basiselementen darstellen.

Beispielsweise:

• {a} gehört bereits zu B.
• {b, c} gehört ebenfalls zu B.
• {a, b, c} ergibt sich als Vereinigung beider Mengen: $$ \{ a,b,c \} = \{ a \} \cup \{ b,c \} $$

Hinweis. Die leere Menge (Ø) ist per Definition ein uneigentliches Teilmengenelement jeder Menge. Daher gehört sie stets zur Topologie: $$ \emptyset \in T $$. Außerdem gilt: Die leere Menge ist in jeder Topologie offen.

Dieses Beispiel veranschaulicht, wie eine Basis im einfachsten Fall funktioniert. In unendlichen oder komplexeren Räumen kann die Konstruktion einer Basis anspruchsvoller sein, doch das Grundprinzip bleibt gleich: Eine Basis liefert die Bausteine, aus denen sich alle offenen Mengen zusammensetzen lassen.

Eine alternative Basis

Man kann dieselbe Topologie auch mit einer anderen Basis beschreiben, etwa:

$$ B = \{ \{ a \}, \{ b \}, \{ c \} \} $$

Diese Basis besteht aus den einelementigen Mengen von X. Prüfen wir, ob sie eine gültige Basis für die Topologie

$$ T = \{ \varnothing, X, \{a\}, \{b,c\} \} $$

bildet:

• Die leere Menge \( \varnothing \) ist per Definition offen und stets enthalten.
• Die Menge \( \{a\} \) gehört direkt zu \( B \).
• Die Menge \( \{b,c\} \) lässt sich als Vereinigung der Mengen \( \{b\} \) und \( \{c\} \) darstellen: $$ \{ b,c \} = \{ b \} \cup \{ c \} $$
• Die gesamte Menge \( X = \{a,b,c\} \) entsteht als Vereinigung aller Elemente von B: $$ \{ a,b,c \} = \{ a \} \cup \{ b \} \cup \{ c \} $$

Damit ist \( B \) eine gültige Basis der Topologie auf X. Dieses Beispiel zeigt, dass eine Topologie mehrere verschiedene Basen haben kann, die alle denselben Raum beschreiben.

Beispiel aus der reellen Zahlengeraden

In der gewohnten Topologie der reellen Zahlen besteht die Standardbasis aus allen offenen Intervallen:

$$ B = \{ (a,b) \subseteq \mathbb{R} \mid a < b \} $$

Jeder Punkt der reellen Achse liegt in mindestens einem solchen Intervall. Schneiden sich zwei offene Intervalle, so enthält ihr Schnitt wiederum ein kleineres offenes Intervall, das ebenfalls zur Basis gehört.

Zum Beispiel: Die Intervalle \( (0,3) \) und \( (2,4) \) schneiden sich im Intervall \( (2,3) \), das zur Basis gehört.

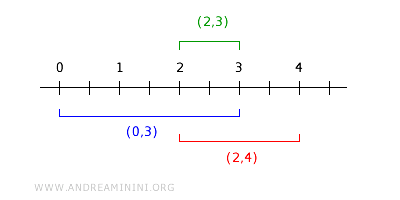
Tatsächlich gilt: $$ (0,3) \cap (2,4) = (2,3) \in B $$

Weitere Bemerkungen

Das Prinzip der Basis lässt sich auf jede Menge anwenden. Nimmt man etwa eine Menge \( X \) und bildet eine Basis \( B \), in der jedes Element \( x \in X \) in einer einelementigen Menge \( \{x\} \in B \) enthalten ist, so kann man daraus beliebige Topologien konstruieren.

Zum Beispiel erzeugt die Basis \( B = \{ \{a\}, \{b\}, \{c\} \} \) für \( X = \{a,b,c\} \) die Topologie \( T = \{ \varnothing, \{a\}, \{b,c\}, X \} \).

Mit derselben Basis lassen sich jedoch auch andere Topologien auf X bilden, etwa:

• \( T = \{ \varnothing, \{b\}, \{a,c\}, X \} \)
• Die triviale Topologie \( T = \{ \varnothing, X \} \)
• Die diskrete Topologie \( T = \{ \varnothing, \{a\}, \{b\}, \{c\}, \{a,b\}, \{a,c\}, \{b,c\}, X \} \)

Hinweis. Die erste Bedingung für eine Basis ist erfüllt, weil jedes Element von \( X \) in mindestens einer Menge aus \( B \) enthalten ist. Die zweite Bedingung gilt ebenfalls, da die Mengen \( \{x\} \) jeweils nur ein Element enthalten und somit disjunkt sind.

Auf diese Weise lässt sich das Konzept der Basis auf beliebige Mengen und Topologien übertragen. Es bildet das Fundament, auf dem ein Großteil der modernen Topologie aufbaut.