Offene Kugel

In der Topologie bezeichnet man eine offene Kugel als die Menge aller Punkte in einem metrischen Raum, die von einem Zentrum $ c $ einen Abstand besitzen, der strikt kleiner ist als ein vorgegebener Radius $ r $ : $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

Die Funktion $ d $ wird als Metrik bezeichnet. Sie misst Abstände innerhalb des Raums und legt damit fest, wie nahe oder weit Punkte voneinander liegen. Eine offene Kugel ist also vollständig durch zwei Angaben bestimmt: ihren Mittelpunkt und ihren Radius.

Sie heißt „offen", weil jeder Punkt im Inneren wiederum das Zentrum einer kleineren Kugel sein kann, die vollständig innerhalb der Ausgangskugel liegt. Dieser Gedanke ist zentral für die Topologie, denn er beschreibt die lokale Struktur des Raums.

Bemerkung: Offene Kugeln bleiben unter Verschiebungen oder maßstäblichen Vergrößerungen und Verkleinerungen unverändert, was ihre topologische Natur betrifft. Ihre Form ist also flexibel, ihr topologisches Verhalten jedoch stabil.

Ein anschauliches Beispiel liefert die euklidische Ebene $ \mathbb{R}^2 $. Der Abstand zwischen einem Punkt $ p = (x, y) $ und einem Zentrum $ c = (x_0, y_0) $ wird durch die bekannte euklidische Formel beschrieben:

$$ d(p,c) = \sqrt{(x - x_0)^2 + (y - y_0)^2} $$

Auf dieser Grundlage bilden offene Kugeln die Basis der üblichen Topologie von $ \mathbb{R}^2 $. Die gesamte Topologie entsteht durch die folgende Menge offener Kugeln:

$$ B = \{ B(p, r) \mid p \in \mathbb{R}^2,\ r > 0 \} $$

Topologie mit offenen Kugeln in R^2

Unter allen denkbaren Topologien auf $ \mathbb{R}^2 $ ist diese die weitaus wichtigste, da sie direkt aus der geometrischen Struktur der Ebene hervorgeht und sich eng an unsere Anschauung von Abständen anlehnt.

In jeder offenen Kugel $ B(p,r) $ lässt sich ein zentrales Prinzip beobachten: Für jeden Punkt $ q \in B(p,r) $ existiert eine kleinere Kugel $ B(q,\epsilon) $, die vollständig in $ B(p,r) $ enthalten ist.

Formal ausgedrückt bedeutet das:

$$ \forall\ q \in B(p,r),\ \exists\ \epsilon > 0\ \text{mit}\ B(q,\epsilon) \subset B(p,r) $$

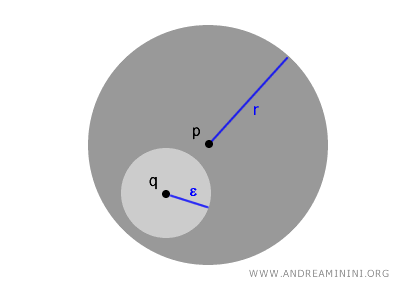
Darstellung einer offenen Kugel

Dieses Prinzip lässt sich beliebig oft wiederholen. So wird deutlich, dass offene Kugeln Bausteine der Topologie sind, die das lokale Verhalten eines Raums prägen und ermöglichen, seine Struktur von innen heraus zu verstehen.