Rand einer Menge
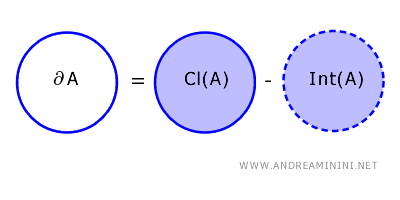
Der Rand einer Teilmenge \( A \) eines topologischen Raums \( X \) umfasst alle Punkte, die zur Adhärenz von \( A \) gehören, aber nicht zu seinem Inneren. Mathematisch lässt sich das kompakt ausdrücken als: \[ \partial A = \text{Cl}(A) - \text{Int}(A) \]
Die Adhärenz \( \text{Cl}(A) \) besteht aus allen Punkten der Menge und ihren Häufungspunkten. Das Innere \( \text{Int}(A) \) hingegen enthält nur jene Punkte, die eine Umgebung besitzen, die vollständig in \( A \) liegt.
Wichtig ist, dass der Rand nicht allein von der Menge, sondern von der Topologie abhängt. Dieselbe Menge kann also je nach Topologie unterschiedliche Ränder besitzen.
Anschaulich gesprochen liegt ein Randpunkt genau dort, wo jede Umgebung zugleich Punkte aus \( A \) und aus dem Komplement \( X \setminus A \) enthält.
Ein konkretes Beispiel
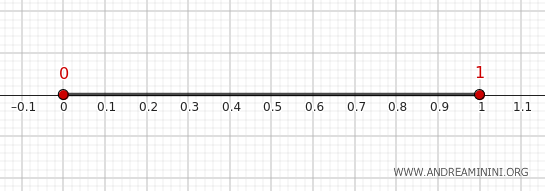
Wir betrachten das offene Intervall \( A = (0, 1) \) in den reellen Zahlen \( \mathbb{R} \) mit der Standardtopologie. Schritt für Schritt bestimmen wir Adhärenz, Inneres und Rand.
1] Adhärenz von A
Zur Adhärenz gehören alle Punkte von \( A \) und sämtliche Häufungspunkte. Für \( (0, 1) \) ergibt sich das abgeschlossene Intervall:
$$ \text{Cl}(A) = [0, 1] $$
2] Inneres von A
Das Innere umfasst nur jene Punkte, die Umgebungen besitzen, die vollständig in \( A \) liegen. Da \( (0, 1) \) offen ist, gilt:
$$ \text{Int}(A) = (0, 1) $$
3] Rand von A
Der Rand entsteht durch den Unterschied zwischen Adhärenz und Innerem:
$$ \partial A = [0, 1] - (0, 1) = \{0, 1\} $$
Die Punkte 0 und 1 sind also die einzigen Randpunkte. Jede Umgebung dieser Punkte enthält sowohl Elemente des Intervalls als auch Elemente außerhalb davon.
Randkriterium
Ein Punkt gehört genau dann zum Rand, wenn jede seiner Umgebungen sowohl \( A \) als auch dessen Komplement trifft.
Dieses Kriterium ist besonders nützlich, wenn man den Rand einzelner Punkte untersuchen oder Ränder in allgemeineren Räumen bestimmen möchte.
Beispiel
Für \( A = (0, 1) \) kennen wir bereits Adhärenz und Inneres:
$$ \text{Cl}(A) = [0, 1], \qquad \text{Int}(A) = (0, 1) $$
Damit lautet der Rand:
$$ \partial A = \{0, 1\} $$
Überprüfung der Randpunkte
Für eine Umgebung von 0 wie \( (0 - \epsilon, 0 + \epsilon) \) gilt: Sie enthält sowohl Punkte aus \( (0,1) \) als auch Punkte \( \le 0 \). Dasselbe gilt für jede Umgebung von 1. Beide Punkte liegen also tatsächlich im Rand.
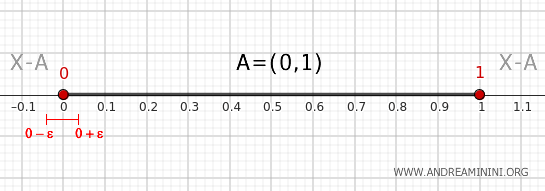
Ein Punkt wie 0.5 hingegen besitzt Umgebungen, die vollständig im Intervall liegen. Deshalb gehört er nicht zum Rand.
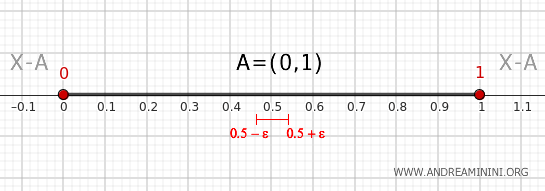
Wichtige Eigenschaften
Die folgenden Aussagen fassen zentrale topologische Eigenschaften des Randes zusammen.
- \( \partial A \subseteq A \) genau dann, wenn \( A \) abgeschlossen ist:
\[ \partial A \subseteq A \Leftrightarrow A \text{ ist abgeschlossen} \] - \( \partial A \cap A = \emptyset \) genau dann, wenn \( A \) offen ist:
Offene Mengen enthalten keine eigenen Randpunkte.
\[ \partial A \cap A = \emptyset \Leftrightarrow A \text{ ist offen} \] - Der Rand ist genau dann leer, wenn die Menge clopen ist:
\[ \partial A = \emptyset \Leftrightarrow A \text{ ist clopen} \] - Der Rand ist die Schnittmenge beider Adhärenzen:
\[ \partial A = \text{Cl}(A) \cap \text{Cl}(X - A) \] - Der Rand ist immer abgeschlossen:
Der Schnitt zweier abgeschlossener Mengen bleibt abgeschlossen, daher ist auch der Rand stets eine abgeschlossene Menge.
- Rand und Inneres überschneiden sich nie:
\[ \partial A \cap \text{Int}(A) = \emptyset \] - Rand und Inneres ergeben zusammen die Adhärenz:
\[ \partial A \cup \text{Int}(A) = \text{Cl}(A) \]
Diese Eigenschaften bilden die Grundlage dafür, wie der Rand in verschiedenen topologischen Räumen analysiert und genutzt wird.