Topologische Transformationen

Topologische Transformationen sind Abbildungen auf topologischen Räumen, die grundlegende Eigenschaften wie Zusammenhang und Stetigkeit unverändert lassen.

Sie bilden einen Kernbereich der Topologie - jenes Zweigs der Mathematik, der untersucht, welche Strukturen und Eigenschaften von Räumen bei stetigen Verformungen erhalten bleiben.

Typische Merkmale topologischer Transformationen sind:

• Stetigkeit
  Eine topologische Transformation muss stetig sein: Kleine Änderungen im Ausgangspunkt führen zu kleinen Änderungen im Bildpunkt.
• Zusammenhang und Nähe
  Begriffe wie Nachbarschaft und Zusammenhang bleiben gewahrt. Sind zwei Punkte im Ausgangsraum benachbart oder verbunden, so gilt dies auch im transformierten Raum.
• Verformung ohne Risse oder Verklebungen
  Objekte dürfen gedehnt, gestaucht oder gebogen werden, jedoch weder zerreißen noch zusammengeklebt werden. So lässt sich etwa ein Donut in eine Kaffeetasse überführen, da beide genau ein "Loch" besitzen.

Anwendungen: Topologische Transformationen finden breite Verwendung - von der reinen Mathematik, etwa in Knotentheorie und algebraischer Topologie, bis hin zur Untersuchung invarianten Verhaltens unter stetigen Deformationen.

Arten topologischer Transformationen

In der Topologie unterscheidet man Transformationen danach, welche Eigenschaften sie erhalten.

Zu den grundlegenden Typen zählen:

• Homöomorphismen
  Ein Homöomorphismus ist eine stetige Abbildung mit einer stetigen Umkehrabbildung. Er erlaubt es, einen Raum in einen anderen zu überführen und diesen Prozess ohne "Risse" oder "Klebungen" rückgängig zu machen. Klassisches Beispiel: die Entsprechung zwischen Tasse und Donut.
• Isotopien
  Eine Isotopie ist ein spezieller Homöomorphismus, bei dem jeder Zwischenschritt selbst ein Homöomorphismus ist. Man denke an das Verschieben eines Knotens entlang einer Schnur, ohne ihn enger oder lockerer zu machen - jede Zwischenstellung ist eine Isotopie.
• Homotopien
  Sie zeigen, wie eine Funktion stetig in eine andere überführt werden kann, wobei zentrale topologische Eigenschaften erhalten bleiben. Homotopie ist weniger streng als Homöomorphismus. Beispiel: Eine Feder wird gestreckt und kehrt dann in ihre Ausgangslage zurück - die Zwischenformen sind homotop.
• Diffeomorphismen
  Ein Diffeomorphismus ist ein Homöomorphismus, der zusätzlich differenzierbar ist. Besonders in der Differentialtopologie spielt dies eine Rolle, wenn Glattheit und Differenzierbarkeit entscheidend sind - etwa beim Übergang von einer Kugel zu einem Ellipsoid.

Diese Typen beleuchten unterschiedliche Facetten von Stetigkeit und Verformbarkeit in der Topologie.

Ihre Anwendung variiert je nach Kontext - ob in allgemeiner, algebraischer oder Differentialtopologie.

Unterschied zwischen geometrischen und topologischen Transformationen

Geometrische und topologische Transformationen unterscheiden sich in ihren Eigenschaften und Zielsetzungen:

• Geometrische Transformationen
  Sie verändern Objekte im Raum, wobei geometrische Größen wie Abstände, Winkel und Formen erhalten bleiben. Beispiele sind Translation, Rotation, Spiegelung und Skalierung.

  Eine Drehung etwa bewahrt Abstände und Winkel, verändert jedoch die Orientierung.

• Topologische Transformationen
  Sie verändern Räume so, dass topologische Eigenschaften wie Zusammenhang und Stetigkeit erhalten bleiben - Abstände oder Winkel jedoch nicht zwingend. Sie sind besonders flexibel, da sie Dehnen und Verformen zulassen, ohne dass geschnitten oder geklebt wird.

  So kann ein Donut topologisch in eine Kaffeetasse überführt werden, da beide ein einziges Loch aufweisen.

Während geometrische Transformationen Bewegungen und Formänderungen beschreiben, die bestimmte Maße und Proportionen wahren, liegt bei topologischen Transformationen der Fokus auf Verformungen, die Zusammenhang und Stetigkeit sichern - unabhängig von Gestalt oder Größe.

Können Transformationen sowohl geometrisch als auch topologisch sein?

Ja. Manche Transformationen bewahren nicht nur geometrische Eigenschaften wie Winkel, Längen und Formen, sondern sind zugleich stetig und sichern damit auch topologische Eigenschaften wie Zusammenhang und Stetigkeit.

Typische Beispiele:

• Isometrien
  Isometrien - etwa Translationen, Drehungen und Spiegelungen - bewahren Abstände und Winkel. Damit sind sie zugleich geometrische wie topologische Transformationen. Sie sind Homöomorphismen, da sie eine stetige Umkehrabbildung besitzen.
  
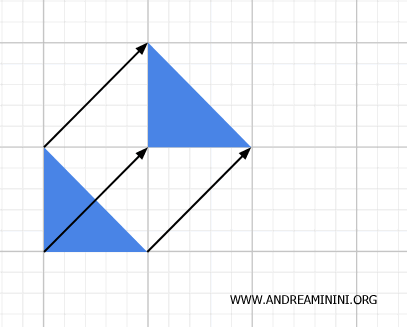
• Ähnlichkeiten
  Ähnlichkeitstransformationen verändern die Größe eines Objekts, erhalten jedoch die Form. Streckungen oder Stauchungen bewahren Winkel und Proportionen. Damit sind sie geometrisch relevant, aber auch topologisch gültig, da sie stetig sind und Zusammenhang erhalten.

Diese Beispiele verdeutlichen: Geometrische und topologische Eigenschaften sind nicht immer strikt voneinander getrennt. Mitunter kann eine Transformation beides zugleich sein - geometrisch bedeutsam und topologisch zulässig.

Und so weiter.