Reguläre Räume in der Topologie
Ein topologischer Raum \( X \) heißt regulär, wenn er zwei zentrale Bedingungen erfüllt:
- Jede Einelementmenge ist abgeschlossen. Mit anderen Worten: Jeder einzelne Punkt von \( X \) bildet ein abgeschlossenes Teilset.
- Ein Punkt und eine abgeschlossene Menge lassen sich trennen. Für jeden Punkt \( a \in X \) und jede abgeschlossene Menge \( C \subset X \), die \( a \) nicht enthält, existieren zwei disjunkte offene Mengen \( U \) und \( V \) mit \[ a \in U, \quad C \subset V, \quad U \cap V = \emptyset \]
Reguläre Räume weisen eine stärkere Trennungseigenschaft auf als Hausdorff-Räume. Die Topologie bietet hier mehr Kontrolle darüber, wie sich Punkte und Mengen durch offene Umgebungen voneinander isolieren lassen.
Besitzt ein regulärer Raum zusätzlich eine abzählbare Basis, so folgt aus dem Satz von Urysohn, dass er metrisierbar ist. Dann lässt sich seine Struktur vollständig durch eine Metrik beschreiben.
Abgrenzung zu Hausdorff-Räumen
Der entscheidende Unterschied liegt im Trennungsniveau: In einem Hausdorff-Raum müssen sich lediglich zwei verschiedene Punkte durch offene Mengen trennen lassen. Ein regulärer Raum verlangt dagegen, dass sogar ein einzelner Punkt und eine abgeschlossene Menge klar isolierbar sind. Die Regularität stellt daher eine strengere Forderung dar.
Hinweis. Ein regulärer Raum ist nicht automatisch ein normaler Raum. Für normale Räume gilt eine noch stärkere Forderung: Zwei disjunkte abgeschlossene Mengen müssen sich ebenfalls durch offene Umgebungen trennen lassen. Jeder normale Raum ist regulär, doch nicht jeder reguläre Raum ist normal.
Regularität ist nur eine von mehreren Trennungseigenschaften. Es existieren reguläre Räume, die nicht Hausdorff sind, ebenso wie Hausdorff-Räume, die nicht regulär sind. Die Trennungsaxiome bilden ein ganzes Spektrum an Feinheitsstufen in der Topologie.
Ein anschauliches Beispiel
Ein besonders zugängliches Beispiel ist die reelle Gerade \( \mathbb{R} \) mit ihrer Standardtopologie. Sie erfüllt die Regularitätseigenschaft auf natürliche Weise.
Betrachten wir den Punkt \( x = 2 \) und die abgeschlossene Menge
\[ C = (-\infty, 0] \cup [5, \infty) \]
Es gilt offensichtlich \( x \notin C \), und \( C \) ist abgeschlossen.

Das Komplement von \( C \) ist offen. Darin finden wir ein Intervall, das den Punkt \( x \) enthält, zum Beispiel \( (0, 5) \).
\[ (a, b) = (0, 5) \]
Nun wählen wir zwei Zahlen \( c \) und \( d \) mit
\[ 0 < c < 2 < d < 5 \]
wobei etwa \( c = 1 \) und \( d = 3 \) geeignet sind.
Damit können wir offene Mengen definieren:
- \( U = (1, 3) \) enthält den Punkt \( x = 2 \).
- \( V = (-\infty, 1) \cup (3, \infty) \) enthält die Menge \( C \).
Die Mengen \( U \) und \( V \) schneiden sich nicht, also \( U \cap V = \emptyset \). Genau dieses Verhalten fordert die Definition eines regulären Raumes.
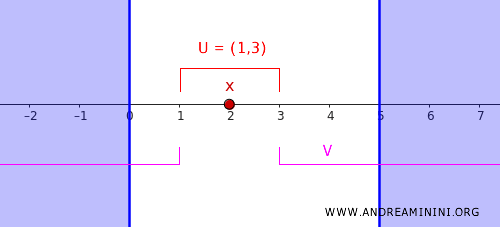
Damit ist gezeigt: Auf der reellen Achse lassen sich Punkte und disjunkte abgeschlossene Mengen durch offene Umgebungen sauber trennen. Die Standardtopologie auf \( \mathbb{R} \) liefert somit ein prototypisches Beispiel für einen regulären Raum.
Zusammenfassung
Trennungsaxiome wie Hausdorff, regulär oder normal geben Auskunft darüber, wie fein eine Topologie strukturiert ist. Je stärker das Trennungsprinzip, desto präziser lassen sich Punkte und Mengen voneinander unterscheiden. Reguläre Räume markieren dabei eine wichtige Stufe in dieser Hierarchie.
Bemerkung. Anschaulich lässt sich sagen: Hausdorff trennt Punkte, Regularität trennt Punkte von abgeschlossenen Mengen. Solche Eigenschaften bestimmen die trennende Auflösung eines Raumes und damit die Klarheit seiner topologischen Struktur.
Und so weiter.