Topologie offener Mengen
Eine Topologie T auf einer Menge X ist eine Familie von Teilmengen von X, die als „offen“ bezeichnet werden und die folgenden Bedingungen erfüllt:
- Die leere Menge Ø sowie die Menge X selbst sind per Definition offen.
- Die Vereinigung beliebig vieler offener Mengen und der Durchschnitt endlich vieler offener Mengen sind ebenfalls offen.
Mit anderen Worten: Die Familie T enthält ausschließlich Teilmengen von X, die als „offen“ gelten, und ist unter den Operationen Vereinigung und Durchschnitt abgeschlossen.
Eine Mengenfamilie ist also eine Menge, deren Elemente wiederum Mengen oder Teilmengen sind.
In diesem Zusammenhang bilden die Menge X und die Topologie T gemeinsam einen topologischen Raum, der üblicherweise als Paar (X,T) notiert wird.
Hinweis. Der Einfachheit halber sagt man oft, X sei ein topologischer Raum. Streng genommen besteht ein topologischer Raum jedoch aus zwei Bestandteilen: der Topologie T (Familie von Teilmengen) und der Grundmenge X.
Warum gilt die leere Menge immer als offen?
Die leere Menge wird in jedem topologischen Raum definitionsgemäß als offen betrachtet.
Diese Konvention gehört zu den Grundannahmen der Topologie und stellt sicher, dass ihre Axiome und Eigenschaften konsistent und vollständig bleiben.
Ein praktisches Beispiel
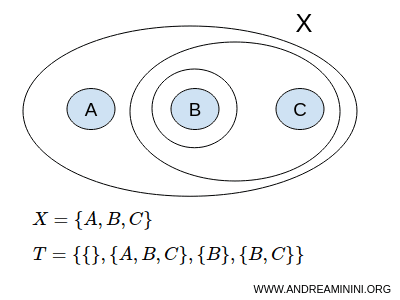
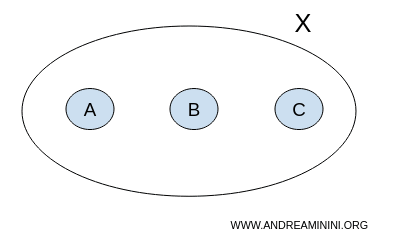
Betrachten wir die Menge X mit den drei Elementen A, B, C
$$ X = \{ A,B,C \} $$
Eine mögliche Topologie T könnte aus den Teilmengen { }, {A,B,C}, {B}, {B,C} bestehen.
$$ T = \{ \{ \},\{A,B,C \}, \{ B \}, \{ B,C \} \} $$
Hierbei steht { } für die leere Menge Ø, während {A,B,C} die gesamte Menge, also die uneigentliche Teilmenge von X darstellt.
Nach Definition sind sowohl die leere Menge als auch die vollständige Menge X offene Mengen.
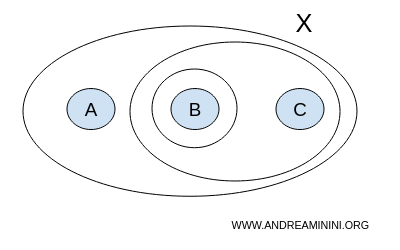
Eine Topologie besteht ausschließlich aus offenen Mengen und ist definitionsgemäß unter Vereinigung und Durchschnitt abgeschlossen.
In diesem Beispiel bleibt jede Vereinigung der in T enthaltenen Teilmengen ebenfalls in T.
Damit ist T unter der Vereinigung abgeschlossen.
$$ \{ B \} \cup \{ B, C \} \subseteq \{ B, C \} \subseteq T$$
$$ \{ B \} \cup \{ A, B, C \} \subseteq \{ A, B, C \} \subseteq T$$
$$ \{ B \} \cup \{ \} \subseteq \{ B \} \subseteq T $$
$$ \{ B \} \cup \{ B \} \subseteq \{ B \} \subseteq T$$
Auch der Durchschnitt von Teilmengen aus T bleibt in T enthalten.
Folglich ist T ebenso unter dem Durchschnitt abgeschlossen.
$$ \{ B \} \cap \{ B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ A, B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ \} \subseteq \{ \} \subseteq T $$
$$ \{ B \} \cap \{ B \} \subseteq \{ B \} \subseteq T$$
Damit erfüllt T sämtliche notwendigen Bedingungen und ist eine Topologie auf X.
Beispiel 2
Betrachten wir nun eine leicht veränderte Familie im Vergleich zum ersten Beispiel.
Die Menge X bleibt unverändert.
$$ X = \{ A,B,C \} $$
Diesmal enthält T jedoch zusätzlich die Teilmenge {A}, neben { }, {A,B,C}, {B}, {B,C}.
$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$
Diese neue Familie T von Teilmengen stellt keine Topologie auf X dar, da sie nicht alle Bedingungen erfüllt.
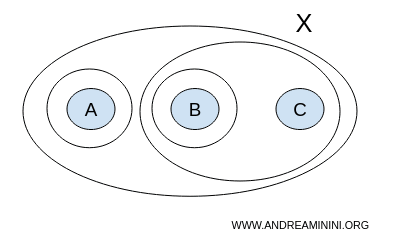
So ergibt etwa die Vereinigung der Teilmengen {A} und {B} die Menge {A,B}, die jedoch nicht in T enthalten ist.
$$\require{cancel} \{ A \} \cup \{ B \} = \{ A, B \} \cancel{\in} T $$
Mit anderen Worten: {A} und {B} gelten in T zwar als „offen“.
Ihre Vereinigung {A,B} liefert jedoch keine weitere offene Menge, da {A,B} nicht zur Familie T gehört.
$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$
Dies widerspricht einer der grundlegenden Bedingungen für eine Topologie auf X.
Daher kann T nicht als Topologie auf X angesehen werden.
Und so weiter