Offene Mengen

Eine Menge A heißt offen, wenn es zu jedem Element x in der Menge (x∈A) eine Umgebung gibt, die vollständig in A enthalten ist.

 

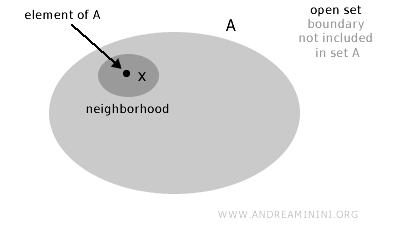
Mit anderen Worten: Eine Menge gilt genau dann als offen, wenn ihre „Randpunkte“ nicht zur Menge selbst gehören.

Formaler ausgedrückt: Eine Menge A in einem topologischen Raum X ist offen, wenn es zu jedem Punkt x in A eine Umgebung von x gibt, die ganz in A enthalten ist.

Hinweis. Das bedeutet: Um jeden Punkt der Menge lässt sich ein Bereich finden, der vollständig in der Menge liegt, ohne den äußeren Rand zu berühren.

Ein praktisches Beispiel

Ein einfaches Beispiel für eine offene Menge auf der Zahlengeraden ist ein offenes Intervall.

Was ist ein offenes Intervall? Ein offenes Intervall in \( \mathbb{R} \) ist die Menge aller reellen Zahlen \( x \), für die \( a < x < b \) gilt. Dabei sind \( a \) und \( b \) zwei reelle Zahlen mit \( a < b \).

Man schreibt dies als (a,b). Die runden Klammern verdeutlichen, dass die Randpunkte a und b nicht zur Menge gehören.

So ist etwa das Intervall (3,10) eine offene Menge auf der reellen Achse.

In diesem Fall besteht A aus unendlich vielen Zahlen zwischen 3 und 10, wobei die Endpunkte ausgeschlossen sind.

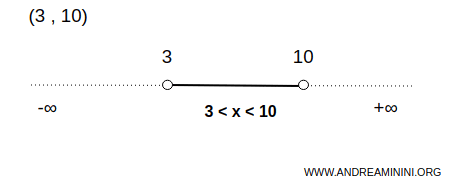
Das heißt: Zu jedem Punkt x in diesem Intervall lässt sich stets ein kleines offenes Intervall um x angeben, das vollständig in (3,10) liegt.

Beispielsweise kann man für x=3,1 das Intervall (3,09;3,11) wählen, das ganz in (3,10) enthalten ist.

Dies gilt für jedes andere Element im Intervall (3,10), da zwischen zwei reellen Zahlen immer unendlich viele weitere liegen.

Hinweis. Selbst wenn ich eine sehr kleine Zahl im Intervall (3,10) betrachte, etwa 3,001, kann ich immer noch eine Umgebung wie 3,001±0,00000001 angeben, die unendlich viele reelle Zahlen im offenen Intervall (3,10) enthält.

Das ist ein anschauliches eindimensionales Beispiel für eine offene Menge.

Weitere Beispiele

Dasselbe Konzept lässt sich auf den zweidimensionalen Raum übertragen.

Zum Beispiel: Die Menge aller Punkte innerhalb eines Kreises mit Radius r=1 und Mittelpunkt im Ursprung (0;0).

$$ x^2+y^2<1 $$

Diese Ungleichung beschreibt alle Punkte, deren Abstand vom Ursprung kleiner als 1 ist. Die Punkte auf dem Kreisrand gehören also nicht dazu - nur die Punkte im Inneren.

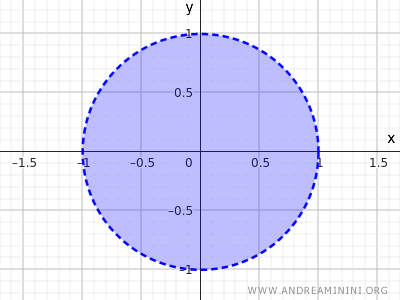
Dies ist ein weiteres Beispiel für eine offene Menge.

Wann ist eine Menge abgeschlossen?

Eine Menge wird abgeschlossen, wenn man zusätzlich die Punkte des Kreisrandes einschließt.

$$ x^2+y^2 \le 1 $$

In diesem Fall gilt die Bedingung, dass jedes Element eine vollständig enthaltene Umgebung besitzt, nicht mehr.

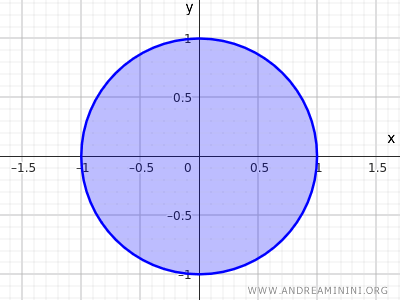
Bei einer abgeschlossenen Menge besitzen die Punkte auf dem Randkreis keine Umgebung, die ganz in der Menge liegt.

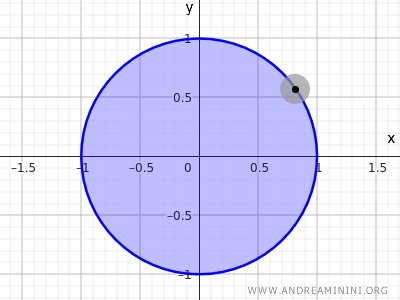
Hinweis. In der Topologie ist die Gleichung $ x^2+y^2=1 $ weder offen noch abgeschlossen im euklidischen Raum R², da sie nur die Randpunkte beschreibt und die inneren Punkte ausschließt. Dagegen ist die Menge $ x^2+y^2<1 $, die die inneren Punkte, aber nicht den Rand enthält, ein Beispiel für eine offene Menge. Fügt man auch die Randpunkte hinzu ($ x^2+y^2\le 1 $), so erhält man eine abgeschlossene Menge.

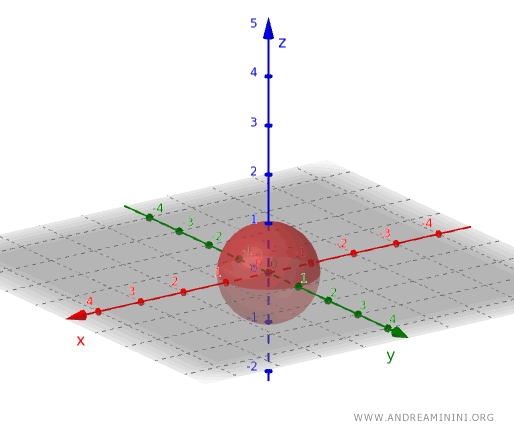
Nach demselben Prinzip erhält man im dreidimensionalen Raum eine offene Menge, wenn man z.B. alle Punkte innerhalb einer Kugel betrachtet, jedoch die Oberfläche ausschließt.

Die Wahl einer Topologie

Offene Intervalle sind nützlich, weil sie anschaulich sind und sofort ein Gefühl dafür vermitteln, was „offen“ bedeutet.

Doch der Begriff der offenen Menge ist weitaus abstrakter und darf nicht nur auf offene Intervalle reduziert werden.

Hat man das Grundprinzip verstanden, sollte man sich eingehender damit beschäftigen.

Ob eine Menge „offen“ ist, hängt von der Topologie ab, die man auf den Raum legt.

Wichtig ist: Die Definition offener Mengen kann je nach gewählter Topologie stark variieren.

In manchen Räumen kann eine Menge, die in der Standardtopologie „abgeschlossen“ erscheint, in einer anderen Topologie durchaus als „offen“ gelten.

Mit anderen Worten: Ob eine Menge offen ist, hängt ausschließlich von der zugrunde liegenden Topologie ab.

Was versteht man unter einer Topologie? Eine Topologie auf einem Raum ist eine Sammlung von Mengen, die nach bestimmten Regeln als „offen“ gelten. Dazu gehört z.B., dass beliebige Vereinigungen offener Mengen wieder offen sind und auch der Schnitt endlich vieler offener Mengen offen bleibt.

Daher sollte man den Blick nicht nur auf die gängigen und leicht verständlichen Beispiele wie offene Intervalle oder Kreisscheiben beschränken.

In der Topologie ist die Definition von „offen“ weit gefasst und umfasst auch Mengen, die auf den ersten Blick gar nicht so wirken.

Ein praktisches Beispiel

Betrachten wir den Raum \( \{a, b\} \) mit nur zwei Elementen.

In diesem Raum lassen sich mindestens zwei verschiedene Topologien definieren: die triviale Topologie und die diskrete Topologie.

• Triviale Topologie
  In der trivialen Topologie auf \( \{a, b\} \) sind nur die leere Menge \( \emptyset \) und der ganze Raum \( \{a, b\} \) offen. Dies ist die einfachste mögliche Topologie, mit praktisch keiner weiteren „offenen Struktur“ außer Raum und Leere.
• Diskrete Topologie
  In der diskreten Topologie ist jede Teilmenge von \( \{a, b\} \) offen. Das heißt, \( \{a\} \), \( \{b\} \), \( \{a, b\} \) und \( \emptyset \) sind alle offen. Die diskrete Topologie ist damit die „reichhaltigste“, weil jede mögliche Teilmenge eine offene Menge bildet.

Betrachten wir nun die Menge \( \{a\} \) in beiden Topologien:

• In der trivialen Topologie ist {a} nicht offen
  Die einzige nichtleere offene Menge ist \( \{a, b\} \).
• In der diskreten Topologie ist {a} offen
  Hier gilt per Definition jede Teilmenge von \( \{a, b\} \) als offen, also auch \( \{a\} \) und \( \{b\} \).

Die Menge \( \{a\} \) ist also in der diskreten Topologie offen, in der trivialen jedoch nicht.

Dieses einfache Beispiel verdeutlicht, wie stark die Definition einer offenen Menge von der gewählten Topologie abhängt.

Satz über offene Mengen

Satz 1

Sei X eine Menge und T eine Topologie auf X. Dann ist eine Teilmenge S ⊂ X genau dann offen, wenn zu jedem Punkt s ∈ S eine Umgebung U existiert, die vollständig in S liegt, also U ⊂ S.

Nach Definition ist S offen, da sie Teil des topologischen Raums (X,T) ist.

Daraus folgt, dass S als die Umgebung jedes ihrer Punkte verstanden werden kann.

Insbesondere gilt: Die Umgebung U_s eines beliebigen Elements s ∈ S ist selbst offen und in S enthalten.

$$ x \in U_s \subset S \subset X $$

Eine offene Menge lässt sich daher als Vereinigung der offenen Umgebungen ihrer Punkte auffassen.

Gilt also: Jeder Punkt s ∈ S besitzt eine Umgebung U_s, die in S enthalten ist, so folgt, dass S offen ist, da es die Vereinigung solcher offenen Mengen darstellt.

Anders formuliert: Eine Menge ist genau dann offen, wenn es zu jedem ihrer Punkte eine Umgebung gibt, die vollständig in der Menge liegt.

Anschauliches Beispiel. Man stelle sich einen Tisch vor, auf dem Glasmurmeln verteilt sind. Jede Murmel entspricht einem Punkt einer Menge. „Offen“ bedeutet hier: Um jede Murmel lässt sich ein Kreis ziehen, der vollständig auf der Tischfläche bleibt, ohne den Rand zu berühren. Gilt dies für alle Murmeln, so bildet die Menge der Murmeln eine offene Menge. Offenheit besagt also, dass um jeden Punkt stets ein Bereich existiert, der noch ganz zur Menge gehört.

Satz 2

Sei \( X \) eine Menge und \( B \) eine Basis einer Topologie auf \( X \). Eine Teilmenge \( A \subset X \) ist genau dann offen in der von \( B \) erzeugten Topologie, wenn zu jedem Punkt \( x \in A \) ein Basiselement \( B_x \in B \) existiert mit \( x \in B_x \) und \( B_x \subseteq A \).

Dieser Satz beschreibt ein zentrales Strukturmerkmal von Topologien, die aus einer Basis hervorgehen.

Das bedeutet: Jeder Punkt einer offenen Menge \( A \) muss in einem Basiselement liegen, das vollständig in \( A \) enthalten ist.

Damit ist gewährleistet, dass \( A \) offen in der durch \( B \) erzeugten Topologie ist.

Beweis. Sei A offen in der durch die Basis B erzeugten Topologie auf X. Dann ist A definitionsgemäß die Vereinigung von Basiselementen. Folglich liegt jedes \( x \in A \) in mindestens einem \( B_x \in B \) mit \( B_x \subset A \). Umgekehrt: Wenn zu jedem \( x \in A \) ein Basiselement \( B_x \) existiert, das ganz in A liegt, so ist A offen. Damit ist die Äquivalenz gezeigt.

Beispiel

Sei \( X = \{1, 2, 3, 4, 5\} \) und \( B = \{\{1\}, \{2,3\}, \{4,5\}\} \) eine Basis. Wir prüfen, ob \( A = \{1,2,3\} \) offen ist.

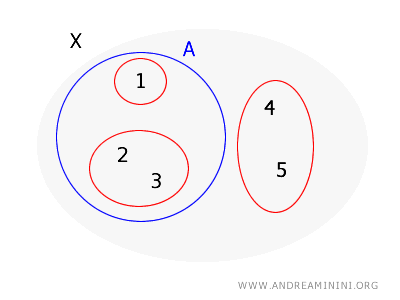
Zu jedem Punkt in \( A \) existiert ein passendes Basiselement:

• Für \( 1 \): \( \{1\} \subset A \).
• Für \( 2 \): \( \{2,3\} \subset A \).
• Für \( 3 \): \( \{2,3\} \subset A \).

Damit erfüllt A die Bedingung, und es folgt: \( A \) ist offen.

Beispiel 2

Mit derselben Basis \( B = \{\{1\}, \{2,3\}, \{4,5\}\} \) betrachten wir nun \( A = \{2,3,4\} \).

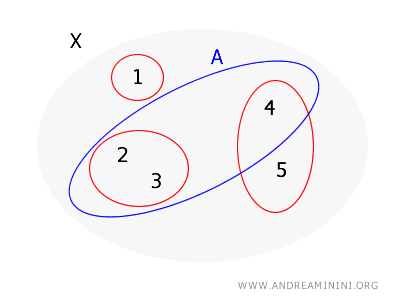
Die Prüfung ergibt:

• Für \( 2 \): \( \{2,3\} \subset A \).
• Für \( 3 \): \( \{2,3\} \subset A \).
• Für \( 4 \): Das einzige Basiselement ist \( \{4,5\} \), doch dieses ist nicht ganz in \( A \), da es 5 enthält.

Also gilt nach dem Satz: \( A \) ist nicht offen, da nicht jeder Punkt ein vollständig in \( A \) enthaltenes Basiselement besitzt.

Bemerkungen

Einige ergänzende Hinweise zu offenen Mengen:

• Eine Menge A ist genau dann offen, wenn A = Int(A)
  Eine Menge \( A \) in einem topologischen Raum \( X \) ist offen, wenn sie mit ihrem Inneren übereinstimmt. Das Innere Int(A) ist die Vereinigung aller offenen Teilmengen von A. $$ A = \text{Int}(A) $$

Weitere Eigenschaften folgen.