Normaler topologischer Raum
Ein topologischer Raum \( X \) heißt normal, wenn zwei zentrale Bedingungen erfüllt sind:
- Jede Einpunktmenge ist abgeschlossen
Das bedeutet, dass für jeden Punkt \( x \in X \) die Menge \(\{x\}\) in der betrachteten Topologie als abgeschlossen gilt. - Disjunkte abgeschlossene Mengen lassen sich durch disjunkte offene Mengen trennen
Sind \( A \) und \( B \) zwei abgeschlossene Teilmengen ohne gemeinsame Punkte (also \( A \cap B = \emptyset \)), so existieren offene Mengen \( U \) und \( V \), die sie trennen. Es gilt:
- \( A \subset U \)
- \( B \subset V \)
- \( U \cap V = \emptyset \)
Die Normalität garantiert, dass man solche disjunkten abgeschlossenen Mengen stets durch offene Umgebungen isolieren kann. Dadurch lassen sich Bereiche eines Raumes sauber voneinander abgrenzen. Diese Eigenschaft ist in vielen Beweisen und Konstruktionen der Topologie unverzichtbar, vor allem wenn man stetige Funktionen definiert, die verschiedene Punkte oder Mengen unterscheiden sollen.
Beispiel
Betrachten wir den Raum \( X = \mathbb{R} \) mit der gewohnten Standardtopologie, die durch offene Intervalle der Form \( (a, b) \) beschrieben wird. Nehmen wir zwei abgeschlossene und disjunkte Teilmengen von \( \mathbb{R} \):
- \( A = \{0\} \), eine Einpunktmenge.
- \( B = [2, 3] \), ein abgeschlossenes Intervall.
Diese beiden Mengen sind abgeschlossen und haben keine gemeinsamen Elemente. Sie sind also disjunkt und erfüllen damit die Ausgangsbedingung.
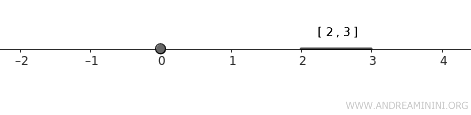
Hinweis. Die Menge \( A \) enthält nur einen Punkt und besitzt kein Inneres. Darum ist sie abgeschlossen. Das Intervall \( B \) ist per Definition abgeschlossen, also ebenfalls eine abgeschlossene Teilmenge.
Um nun die Normalität zu zeigen, suchen wir offene Mengen, die diese abgeschlossenen Mengen trennen. Eine einfache Wahl ist:
$$ A \subset U = (-1,1) $$
und für die zweite Menge:
$$ B \subset V = (1,4) $$
Die offenen Mengen \( U \) und \( V \) schneiden sich nicht, denn es gilt \( U \cap V = \emptyset \). Damit ist die Trennung erreicht.
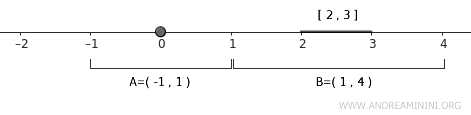
Dieses Vorgehen funktioniert nicht nur in diesem Beispiel, sondern in allen vergleichbaren Situationen. Deshalb ist die reelle Gerade \( \mathbb{R} \) mit ihrer Standardtopologie ein normaler Raum.
Zusätzliche Hinweise
Einige zentrale Informationen zum einordnen:
- Die reellen Zahlen \( \mathbb{R} \) sind normal
Sie erfüllen neben der Regularität auch das stärkere Normalitätskriterium. - Jeder metrische Raum ist normal
Metriken erlauben es, disjunkte abgeschlossene Mengen systematisch zu trennen. Daher gilt die Normalität automatisch. - Normalität impliziert Regularität
Jeder normale Raum ist regulär, aber nicht umgekehrt. Die Normalität ist also die stärkere Eigenschaft.
Diese Eigenschaftskette hat weitreichende Folgen und spielt in vielen Bereichen der Topologie eine fundamentale Rolle.