Digitale Topologie diskreter Räume

Die digitale Topologie (digital topology) befasst sich mit topologischen Strukturen auf diskreten Räumen. Gemeint sind dabei insbesondere Punktgitter wie Pixelanordnungen in zwei Dimensionen oder Voxelsysteme in drei Dimensionen. Im Fokus stehen die Konnektivitätsbeziehungen zwischen Punkten, die durch klar definierte Adjazenzregeln festgelegt werden.

Im Unterschied zur klassischen Topologie werden offene Mengen hier nicht über Abstände oder stetige Umgebungen beschrieben, sondern über die Verbindungen zwischen benachbarten Punkten. Welche Punkte als Nachbarn gelten, hängt vom gewählten Konnektivitätsmodell ab, etwa von der 4er- oder 8er-Konnektivität im zweidimensionalen Fall oder von der 6er-, 18er- beziehungsweise 26er-Konnektivität im dreidimensionalen Raum.

Die digitale Topologie ist von großer praktischer Bedeutung. Sie bildet die theoretische Grundlage vieler Verfahren in der Bildverarbeitung, der Computergrafik und der Computer Vision, da sie zentrale Ideen der klassischen Topologie auf diskrete, rechnerbasierte Strukturen überträgt.

Offene Mengen in der digitalen Topologie

Eine Menge \(U\) heißt in der digitalen Topologie offen, wenn für jeden Punkt \(x \in U\) alle zu \(x\) adjazenten Punkte gemäß der gewählten Konnektivitätsregel ebenfalls zu \(U\) gehören.

Der Begriff der „Adjazenz" oder „Nachbarschaft" ist dabei kontextabhängig und wird durch das jeweilige Konnektivitätsmodell bestimmt. Typische Beispiele verdeutlichen diesen Zusammenhang:

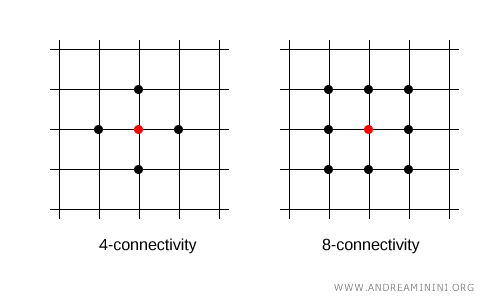
Auf einem kreisförmigen oder ringförmigen Gitter ist jeder Punkt genau mit zwei anderen Punkten verbunden. Man spricht in diesem Fall von einer 2er-Konnektivität.

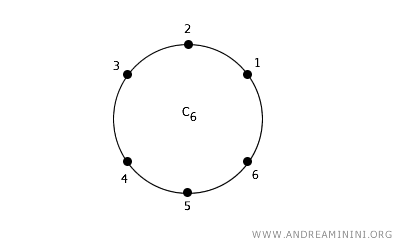
In einer zweidimensionalen Gitterebene kann ein Punkt entweder vier direkte Nachbarn haben, nämlich in Nord-, Süd-, Ost- und West-Richtung (4er-Konnektivität), oder acht Nachbarn, wenn auch die diagonalen Richtungen berücksichtigt werden (8er-Konnektivität).

In einem dreidimensionalen digitalen Raum (3D) wird die Nachbarschaft entsprechend über 6, 18 oder 26 benachbarte Punkte definiert, abhängig davon, wie viele angrenzende Voxeln als verbunden gelten.

Beispiel

Betrachten wir eine Menge von Punkten, die in einem diskreten Raum kreisförmig angeordnet sind und einer 2er-Konnektivität unterliegen.

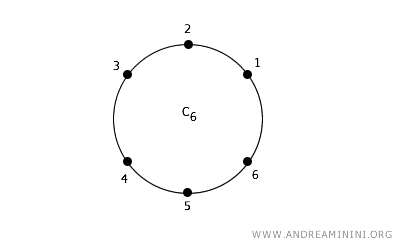
In dieser Anordnung besitzt jeder Punkt genau zwei unmittelbare Nachbarn, einen links und einen rechts.

So ist etwa der Punkt 2 direkt zu den Punkten 1 und 3 adjazent.

Eine Menge \(U\) ist also genau dann offen, wenn alle Nachbarn jedes einzelnen Punktes aus \(U\) ebenfalls zu \(U\) gehören.

Auf diese Weise wird im diskreten Rahmen eine präzise Entsprechung zur intuitiven Vorstellung von lokaler Zusammengehörigkeit und struktureller Kontinuität geschaffen.

Unterschied zwischen digitaler Topologie und diskreter Topologie

Sowohl die digitale Topologie als auch die diskrete Topologie beschäftigen sich mit diskreten Räumen. Dennoch unterscheiden sie sich in einem zentralen Punkt:

• Diskrete Topologie
  Eine Topologie auf einer Menge \(X\) heißt diskret, wenn jede Teilmenge von \(X\) offen ist.
• Digitale Topologie
  In der digitalen Topologie ist eine Teilmenge nur dann offen, wenn sie die vorgegebenen Konnektivitätsbedingungen zwischen den Punkten erfüllt.

Worin besteht also der entscheidende Unterschied ?

In der diskreten Topologie ist jede Teilmenge per Definition offen. In der digitalen Topologie hingegen werden nur diejenigen Mengen als offen angesehen, die den festgelegten Nachbarschafts- und Konnektivitätsregeln entsprechen.

Mit anderen Worten: Die digitale Topologie ist nicht mit der diskreten Topologie gleichzusetzen, da nicht jede Teilmenge automatisch offen ist.

So ist beispielsweise eine Menge aus zwei isolierten Pixeln ohne Verbindung in der digitalen Topologie nicht offen, während sie in der diskreten Topologie als offen gilt.

Zusammenfassend lässt sich sagen, dass die digitale Topologie gezielt die Konnektivität zwischen Punkten in einem digitalen Raum modelliert, während die diskrete Topologie jeden Punkt als unabhängige Einheit ohne Nachbarschaftsbeziehungen betrachtet.

Beispiel

Betrachten wir die Punktmenge \(\{1, 2, 3, 4\}\), die kreisförmig angeordnet ist, mit einer digitalen Topologie auf Basis einer 2er-Konnektivität.

• Die Menge \(\{1, 2\}\) ist in der digitalen Topologie offen, da die Punkte 1 und 2 direkt adjazent sind.
• Die Menge \(\{1, 3\}\) ist nicht offen, da zwischen den Punkten 1 und 3 keine direkte Verbindung besteht.

Werden dieselben Punkte \(\{1, 2, 3, 4\}\) hingegen im Rahmen einer diskreten Topologie betrachtet, so sind sowohl \(\{1, 2\}\) als auch \(\{1, 3\}\) offen, da dort jede Teilmenge offen ist.

Hinweis. Im selben diskreten metrischen Raum \(\{1, 2, 3, 4\}\) ist die digitale Topologie restriktiver als die diskrete Topologie, da sie für offene Mengen eine explizite Konnektivitätsbedingung verlangt.

Und so weiter.