Clopen-Mengen
Eine Menge wird als "clopen" bezeichnet, wenn sie in einer gegebenen Topologie zugleich offen und abgeschlossen ist.
Mit anderen Worten: Eine clopen-Menge erfüllt gleichzeitig die Bedingungen dafür, offen und abgeschlossen in der betrachteten Topologie zu sein.
Der Ausdruck "clopen" ist ein Kunstwort, das sich aus den Begriffen "closed" (abgeschlossen) und "open" (offen) zusammensetzt.
Solche Mengen besitzen Eigenschaften sowohl von offenen Mengen als auch von abgeschlossenen Mengen.
Dies tritt genau dann ein, wenn sowohl eine Menge als auch ihr Komplement in der gegebenen Topologie offen sind.
Hinweis: In den reellen Zahlen kommen clopen-Mengen nur sehr selten vor, in anderen topologischen Räumen jedoch durchaus. Sie sind besonders interessant, weil sie spezielle Eigenschaften zeigen und eine zentrale Rolle beim Verständnis der topologischen Struktur eines Raumes spielen.
Ein Konkretes Beispiel
Betrachten wir die Menge \(X=\{a,b,c,d\}\) mit einer Topologie \(T\).
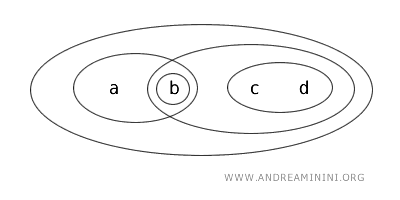
Unter der Topologie \(T\) gelten die folgenden Mengen als offen: \(\{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, \{a,b,c,d\}, \varnothing\).
Daraus folgt, dass die Teilmenge \(\{a,b\}\) in dieser Topologie \(T\) eine offene Menge ist.
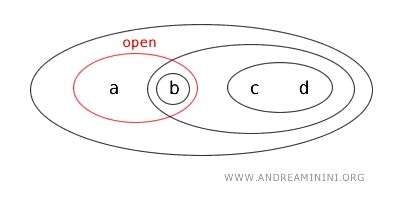
Auffällig ist zudem: Die Menge \(\{a,b\}\) ist zugleich das Komplement der offenen Menge \(\{c,d\}\):
$$ X - \{ c,d \} = \{a , b \} $$
Da das Komplement einer offenen Menge stets abgeschlossen ist, gilt:
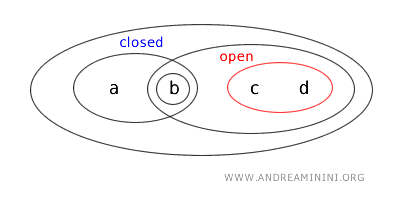
Damit ist die Menge \(\{a,b\}\) zugleich eine abgeschlossene Menge.
Insgesamt ergibt sich also: Innerhalb der Topologie \(T\) ist die Menge \(\{a,b\}\) sowohl offen als auch abgeschlossen - also clopen.
Die Leere Menge und die Gesamtheit sind Clopen
In jeder Topologie auf einer Menge \(X\) sind sowohl die Gesamtheit (\(X\)) als auch die leere Menge (\(\varnothing\)) immer clopen, das heißt zugleich offen und abgeschlossen.
Eine Menge gilt als clopen, wenn sie gleichzeitig die Definitionen von offener und abgeschlossener Menge in der betrachteten Topologie erfüllt.
Um dies besser zu verstehen, erinnern wir uns kurz an die Definitionen von offen und abgeschlossen.
Nach der topologischen Definition sind sowohl die leere Menge (\(\varnothing\)) als auch die Gesamtheit (\(X\)) stets offen.
Ebenso gilt: Eine Menge ist abgeschlossen, wenn ihr Komplement offen ist.
Daraus lässt sich direkt schließen:
- Leere Menge (\(\varnothing\))
Nach den Grundaxiomen der Topologie ist die leere Menge offen. Gleichzeitig ist sie abgeschlossen, da ihr Komplement \(X \setminus \varnothing = X\) (die Gesamtheit) offen ist. Somit ist die leere Menge sowohl offen als auch abgeschlossen, also clopen. - Gesamtheit (\(X\))
Die Gesamtheit ist definitionsgemäß offen. Gleichzeitig ist sie abgeschlossen, da ihr Komplement \(X \setminus X = \varnothing\) (die leere Menge) offen ist. Daher ist auch die Gesamtheit clopen.
Folglich sind in jeder Topologie sowohl die Gesamtheit \(X\) als auch die leere Menge \(\varnothing\) clopen-Mengen.
Und so weiter.