Mengen, die weder offen noch abgeschlossen sind

In der Topologie bezeichnet man eine Menge als weder offen noch abgeschlossen, wenn sie die Kriterien für keine dieser beiden Klassen erfüllt.

Dies tritt in einer Topologie genau dann auf, wenn die betrachtete Menge weder als offene Menge vorkommt noch mit dem Komplement einer solchen übereinstimmt.

Damit kann eine solche Menge auch nicht als abgeschlossene Menge gelten.

Hinweis: In der Standardtopologie der reellen Zahlen ist es wenig anschaulich, sich Mengen vorzustellen, die weder offen noch abgeschlossen sind. In allgemeineren topologischen Räumen hingegen sind solche Beispiele völlig natürlich. Ein konkretes Beispiel veranschaulicht das Konzept deutlich besser.

Ein Beispiel

Betrachten wir die Menge \( X = \{a,b,c,d\} \) und eine Topologie \( T \), in der folgende Mengen als offen definiert sind: \( \{b\} \), \( \{a,b\} \), \( \{c,d\} \), \( \{b,c,d\} \), \( \{a,b,c,d\} \) sowie die leere Menge (\(\varnothing\)).

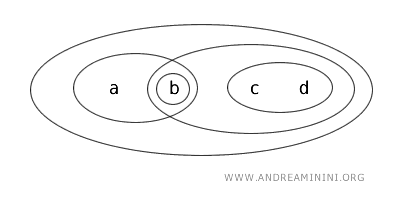
Untersuchen wir nun die Teilmenge \( \{b,c\} \) von \( X \).

• Die Menge \( \{b,c\} \) ist nicht offen in der Topologie \( T \), da sie nicht explizit in der Liste der offenen Mengen enthalten ist.
• Ebenso ist \( \{b,c\} \) nicht abgeschlossen, weil ihr Komplement \( X \setminus \{b,c\} = \{a,d\} \) ebenfalls nicht zu den offenen Mengen von \( T \) gehört.

Wir sehen also: In der Topologie \( T \) ist die Menge \( \{b,c\} \) weder offen noch abgeschlossen.

Und so weiter.