Konvergenz in einem topologischen Raum

In einem topologischen Raum $ X $ nennt man einen Punkt $ x \in X $ den Grenzwert einer Folge $ (x_n) $, wenn zu jeder Umgebung $ U $ von $ x $ eine natürliche Zahl $ N $ existiert, sodass für alle $ n \geq N $ gilt: $ x_n \in U $.

Anschaulich bedeutet das: Eine Folge konvergiert gegen einen Punkt, wenn ihre Folgenglieder ab einem bestimmten Index dauerhaft in jeder noch so kleinen Umgebung dieses Punktes liegen.

Formal schreibt man:

$$ \lim_{n \to \infty} x_n = x $$

In diesem Fall bezeichnet man $ x $ als den Grenzwert der Folge $ (x_n) $.

Anschauliches Beispiel

Betrachten wir als Beispiel die Folge $ \left( \frac{1}{n} \right) $ im topologischen Raum $ X = \mathbb{R} $, ausgestattet mit der üblichen euklidischen Topologie.

$$ x_n = \left( \frac{1}{n} \right) $$

Wir zeigen nun, dass diese Folge gegen 0 konvergiert, also dass 0 ihr Grenzwert ist.

Sei dazu $ U $ eine beliebige Umgebung von 0.

In der Standardtopologie auf $ \mathbb{R} $ enthält jede Umgebung von 0 ein offenes Intervall der Form $ (-\epsilon, \epsilon) $ mit $ \epsilon > 0 $.

Wir suchen also eine natürliche Zahl $ N \in \mathbb{N} $, sodass für alle $ n \geq N $ gilt: $ \frac{1}{n} \in (-\epsilon, \epsilon) $.

Für ein gegebenes $ \epsilon > 0 $ genügt es,

$$ N = \left\lceil \frac{1}{\epsilon} \right\rceil $$

zu wählen. Dann gilt für alle $ n \geq N $:

$$ n \geq \frac{1}{\epsilon} \quad \Rightarrow \quad \frac{1}{n} \leq \epsilon $$

Damit folgt unmittelbar:

$$ \left| \frac{1}{n} \right| < \epsilon \quad \text{für alle } n \geq N. $$

Das bedeutet: Zu jeder Umgebung $ U $ von 0 existiert ein Index $ N $, ab dem alle Folgenglieder vollständig in $ U $ liegen. Somit gilt:

$$ \lim_{n \to \infty} \frac{1}{n} = 0 $$

Damit ist gezeigt, dass 0 tatsächlich der Grenzwert der Folge $ \left( \frac{1}{n} \right) $ ist.

$$ \lim_{n \rightarrow \infty} \frac{1}{n} = 0 $$

Anders formuliert: Die Folge $ \frac{1}{n} $ nähert sich der Null immer weiter an, da ihre Glieder ab einem gewissen Punkt in jeder noch so kleinen Umgebung von 0 verbleiben.

Zur Veranschaulichung zeigt die folgende Tabelle die ersten zehn Folgenglieder:

$$ \begin{array}{|c|c|} \hline n & \frac{1}{n} \\ \hline 1 & 1 \\ 2 & 0.5 \\ 3 & 0.333 \\ 4 & 0.25 \\ 5 & 0.2 \\ 6 & 0.167 \\ 7 & 0.143 \\ 8 & 0.125 \\ 9 & 0.111 \\ 10 & 0.1 \\ \hline \end{array} $$

Wählt man beispielsweise $ N = 5 $, also $ x_5 = \frac{1}{5} = 0.2 $, dann liegen für alle $ n > 5 $ die weiteren Folgenglieder in der Umgebung $ U = (0, 0.2) $.

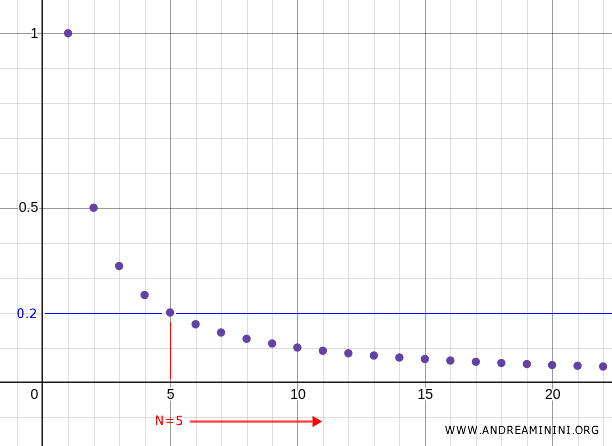
Veranschaulichung der Konvergenz einer Zahlenfolge

Dieses Argument funktioniert unabhängig von der konkreten Wahl von $ N $.

Wählt man beispielsweise $ N = 10 $, so ist $ x_{10} = 0.1 $, und für alle $ n > 10 $ liegen die Folgenglieder in der Umgebung $ U = (0, 0.1) $, und so weiter.

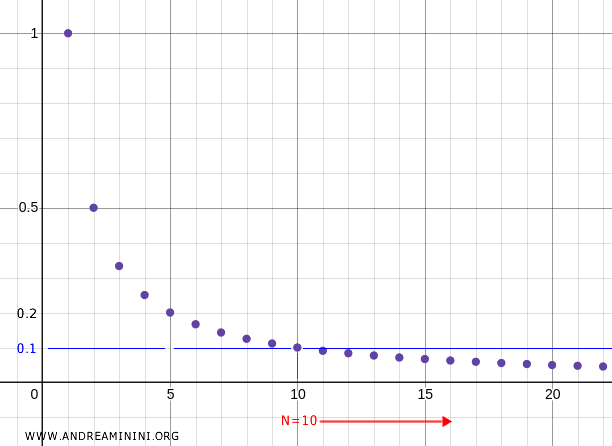
Grafische Darstellung einer konvergenten Folge

Damit ist klar, dass 0 der Grenzwert der Folge ist.

Und so weiter.