Quotiententopologie

Sei $X$ ein topologischer Raum und $A$ eine Menge, die nicht notwendigerweise eine Teilmenge von $X$ ist. Es sei eine surjektive Abbildung $p : X \rightarrow A$ gegeben. Eine Teilmenge $U \subseteq A$ heißt genau dann offen, wenn ihr Urbild $p^{-1}(U)$ in $X$ offen ist.

Einfach gesagt: Eine Menge $U \subseteq A$ ist genau dann offen in der Quotiententopologie, wenn alle Punkte aus $X$, die durch $p$ auf $U$ abgebildet werden, bereits eine offene Menge in $X$ bilden.

anschauliches Schema einer Quotiententopologie

Auf diese Weise erhält die Menge $A$ eine eigene Topologie, die man als Quotiententopologie bezeichnet. Sie wird vollständig durch die Topologie von $X$ und die Abbildung $p$ bestimmt.

Der Raum $A$ heißt in diesem Zusammenhang Quotientenraum, während $p$ als Quotientenabbildung bezeichnet wird.

Die Gesamtheit aller offenen Mengen von $A$ nennt man häufig die „durch $p$ induzierte Quotiententopologie“.

Zusammengefasst gilt: In der Quotiententopologie entscheidet allein das Urbild darüber, ob eine Menge offen ist.

Dabei sollte man eine häufige Fehlannahme vermeiden:

Das Urbild einer offenen Menge im Quotientenraum $A$ ist immer offen in $X$, aber nicht jede offene Menge aus $X$ wird zu einer offenen Menge in $A$.
Das direkte Bild einer offenen Menge aus $X$ kann in $A$ seine Offenheit verlieren, da durch $p$ Punkte zusammengefasst werden.

Ein Quotientenraum entsteht also, indem man in einem topologischen Raum bestimmte Punkte gemäß einer Äquivalenzrelation identifiziert.

Anschaulich gesprochen werden ausgewählte Punkte eines Raumes „zusammengeklebt“, um einen neuen Raum mit veränderter Struktur zu erhalten.

Warum ist die Quotiententopologie nützlich ? Sie erlaubt es, komplexe Räume über einfachere Ausgangsräume zu verstehen und deren Eigenschaften systematisch zu untersuchen.

Erläuterung
Ein konkretes Beispiel
Eigenschaften der Quotiententopologie

Erläuterung

Obwohl der Begriff der Quotiententopologie zunächst abstrakt wirkt, lässt sich die dahinterstehende Idee gut anhand geometrischer Vorstellungen erklären.

Die Quotiententopologie liefert ein formales Werkzeug, um neue Räume zu erzeugen, indem man bestimmte Kanten oder Flächen eines Objekts miteinander identifiziert.

Man denke an ein quadratisches Blatt Papier. Klebt man zwei gegenüberliegende Seiten zusammen, entsteht ein Zylinder.

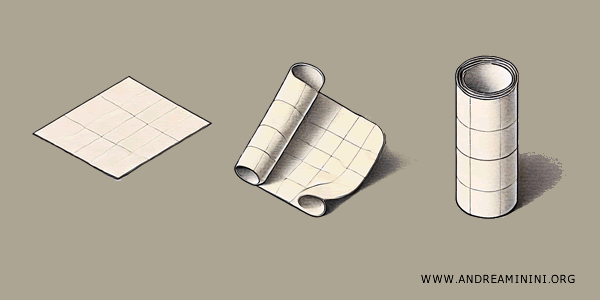
Quadrat wird durch Zusammenkleben zu einem Zylinder

Verbindet man anschließend die beiden kreisförmigen Randlinien des Zylinders, erhält man einen Torus.

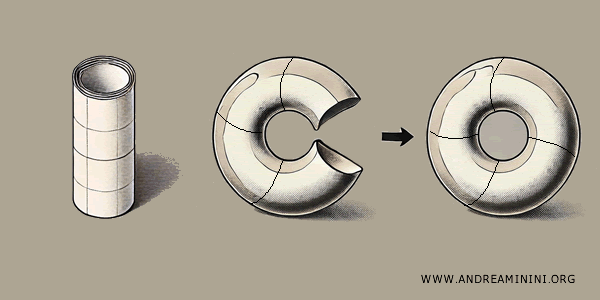
Torus entsteht durch Identifikation der Zylinderränder

In beiden Schritten entsteht eine neue Form allein dadurch, dass bestimmte Randbereiche miteinander identifiziert werden.

Ganz entsprechend erlaubt die Quotiententopologie, neue topologische Räume aus einfachen Ausgangsräumen zu konstruieren.

Diese Methode ist ein zentrales Hilfsmittel, um die globalen Eigenschaften von Flächen und allgemeinen topologischen Räumen zu untersuchen.

Ein konkretes Beispiel

Betrachten wir den Raum $ X = [0, 1] $ mit der üblichen Topologie, in der offene Mengen durch offene Intervalle beschrieben werden.

In diesem Raum gelten unter anderem folgende Eigenschaften:

$X$ und $ \emptyset $ sind per Definition offen.
Jedes offene Intervall $ (a,b) $ mit $ 0 \leq a < b \leq 1 $ ist eine offene Menge in $X$.

Anschaulich lässt sich $X$ als ein Streckenstück zwischen den Punkten $0$ und $1$ darstellen.

Streckenstück als Modell für das Intervall [0,1]

Nun bilden wir einen Quotientenraum, indem wir die beiden Endpunkte $0$ und $1$ identifizieren, also als einen einzigen Punkt betrachten.

Dazu definieren wir die Abbildung $ p : [0, 1] \rightarrow A $ durch:

$$ p(x) = \begin{cases} p(0) & \text{falls } x = 0 \text{ oder } x = 1 \\ \\ x & \text{falls } 0 < x < 1 \end{cases} $$

Der entstehende Raum $A$ lässt sich als ein Kreis interpretieren, bei dem die Endpunkte des Intervalls zusammengefallen sind.

Kreis als Quotient des Intervalls [0,1]

Anschaulich wird das Streckenstück so „gebogen“, dass seine Enden verbunden werden.

Der Punkt $P = \{0,1\}$ steht dabei für das gemeinsame Bild der beiden Endpunkte.

Die Topologie auf $A$ wird nun vollständig über Urbilder festgelegt.

Eine Teilmenge $U \subseteq A$ ist genau dann offen, wenn $p^{-1}(U)$ eine offene Menge in $[0,1]$ ist.

Zwei typische Situationen sind besonders aufschlussreich:

Intervall $ U = (a,b) $ ohne den Punkt $P$
Das Urbild ist ein offenes Intervall in $X$. Daher ist $U$ offen in $A$.
Intervall $ U = (a,b) $ mit dem Punkt $P$
Das Urbild zerfällt in die beiden offenen Intervalle $ [0,a) \cup (b,1] $. Auch hier ist $U$ offen in $A$.

So entsteht aus dem einfachen Intervall $[0,1]$ ein topologischer Kreis.

Dieses Beispiel zeigt anschaulich, wie die Quotiententopologie einen vertrauten Raum in einen neuen, strukturell anderen Raum überführt.

Beispiel 2

Im zweiten Beispiel wird die reelle Zahlengerade auf einen Kreis abgebildet.

Ausgangspunkt ist der Raum $ \mathbb{R} $, der sich unbegrenzt in beide Richtungen erstreckt.

Die Idee besteht darin, jede reelle Zahl auf ihren Nachkommateil zu reduzieren und diesen auf dem Kreis darzustellen.

Dazu verwendet man die Abbildung $ p(x) = x \mod 1 $.

Anschaulich bedeutet dies, dass nur der Dezimalanteil einer Zahl berücksichtigt wird.

So wird etwa $ x = 1{,}3 $ auf den Punkt 0,3 abgebildet. Ebenso entspricht $ x = 2{,}7 $ dem Punkt 0,7 auf dem Kreis.
Darstellung der Modulo-Abbildung von R auf den Kreis

Erhöht man $x$ um eine ganze Zahl, ändert sich sein Bild auf dem Kreis nicht.

Damit werden alle Zahlen identifiziert, die sich um ein ganzzahliges Vielfaches unterscheiden.

Betrachten wir nun einige typische Intervalle.

Intervall (0,1)
Es wird zu einem offenen Kreisbogen. Da sein Urbild offen ist, bleibt es auch im Quotientenraum offen.
Intervall (1,2)
Dieses Intervall wird auf denselben Kreisbogen abgebildet wie (0,1) und liefert daher keine neue Struktur.
Intervall (0,2)
Dieses Intervall überdeckt den gesamten Kreis. Sein Bild ist der ganze Kreis, der hier sowohl offen als auch abgeschlossen ist.

Anmerkung : Das Beispiel zeigt, dass das direkte Bild einer offenen Menge aus $ \mathbb{R} $ im Quotientenraum nicht notwendigerweise offen ist.

Umgekehrt besitzt jede offene Menge des Kreises stets ein offenes Urbild in $ \mathbb{R} $.

Denn das „Abrollen“ eines offenen Kreisbogens ergibt eine Vereinigung offener Intervalle.

Fazit

Die Quotiententopologie macht deutlich, dass Offenheit im Zielraum nicht allein vom Ausgangsraum abhängt, sondern wesentlich von der gewählten Identifikation der Punkte bestimmt wird.

Beispiel 3

In diesem dritten Beispiel sehen wir, wie sich eine Quotiententopologie aus einer endlichen Folge aufeinanderfolgender ganzer Zahlen konstruieren lässt. Dazu identifizieren wir das erste Element $m$ und das letzte Element $n$ der Menge $ \{ m, m+1, \ldots, n \} \subset \mathbb{Z} $.

Betrachten wir konkret die sieben aufeinanderfolgenden ganzen Zahlen von 1 bis 7:

$$ I_7 = \{1, 2, 3, 4, 5, 6, 7\} $$

Diese Menge bildet ein endliches diskretes Intervall. Sie besteht aus aufeinanderfolgenden ganzen Zahlen und trägt die von $ \mathbb{Z} $ induzierte Teilraumtopologie.

Nun identifizieren wir das erste Element (1) mit dem letzten (7). Anschaulich entspricht dies dem Schließen einer offenen Strecke zu einer geschlossenen Schleife.

Darstellung eines endlichen zyklischen Raums durch Identifikation der Intervallendpunkte

Das Ergebnis ist ein endlicher zyklischer Raum, oft auch als endlicher Kreis oder zyklischer Graph bezeichnet. Er besteht aus 6 Punkten, die ringförmig angeordnet sind.

Jeder Punkt besitzt genau zwei unmittelbare Nachbarn. Diese einfache Nachbarschaftsstruktur macht den zyklischen Charakter des Raums deutlich.

Topologisch handelt es sich um einen Quotientenraum, da der neue Raum durch Identifikation von Punkten des ursprünglichen Raums entsteht.

Anmerkung : Formal ist dieses Beispiel analog zur Identifikation der Endpunkte eines reellen Intervalls $(a,b)$. Der wesentliche Unterschied besteht darin, dass hier ein endlicher und diskreter Raum entsteht, während im reellen Fall ein zusammenhängender Raum resultiert.

Der so entstandene endliche Kreis lässt sich außerdem im Rahmen der numerischen Topologie betrachten, in der Nachbarschaftsrelationen explizit festgelegt werden.

In diesem Kontext arbeitet man mit diskreten Räumen, auf die Begriffe wie Zusammenhang und Offenheit in numerischer Interpretation angewendet werden.

Anmerkung : In der numerischen Topologie heißt eine Menge $ U $ offen, wenn für jeden Punkt $ x \in U $ alle zu $ x $ benachbarten Punkte ebenfalls in $ U $ enthalten sind, etwa bei 2-Nachbarschaft in 1D, 4- oder 8-Nachbarschaft in 2D sowie 6- oder 18-Nachbarschaft in 3D.

Wichtig ist, dass Quotiententopologie und numerische Topologie unterschiedlichen theoretischen Rahmen angehören.

Auch wenn der endliche Kreis durch Punktidentifikation entsteht, wird er in der numerischen Topologie als diskreter Raum mit explizit definierter Nachbarschaftsstruktur behandelt.

Beispiel 4

Im nächsten Beispiel betrachten wir die reellen Zahlen $ \mathbb{R} $ mit ihrer üblichen Topologie und definieren eine Quotientenabbildung $ p : \mathbb{R} \to \{a, b, c\} $ durch:

$$ p(x) = \begin{cases} a \quad \text{für } x < 0 \\ \\ b \quad \text{für } x = 0 \\ \\ c \quad \text{für } x > 0 \\ \end{cases} $$

Diese Abbildung kontrahiert alle strikt negativen reellen Zahlen zu einem einzigen Punkt $ a $, bildet den Punkt $0$ auf $ b $ ab und fasst alle strikt positiven reellen Zahlen im Punkt $ c $ zusammen.

Die durch $ p $ induzierte Quotiententopologie auf der Menge $ \{a, b, c\} $ wird vollständig durch die Urbilder dieser drei Punkte bestimmt.

Konkret ergeben sich folgende Urbilder:

$ p^{-1}(a) = (-\infty, 0) $, eine offene Menge in $ \mathbb{R} $,
$ p^{-1}(b) = \{0\} $, die nicht offen ist,
$ p^{-1}(c) = (0, \infty) $, ebenfalls offen.

Nach der Definition der Quotiententopologie ist eine Teilmenge von $ \{a, b, c\} $ genau dann offen, wenn ihr Urbild unter $ p $ offen in $ \mathbb{R} $ ist. Daraus folgt, dass die folgenden Mengen offen sind:

das Singleton $ \{a\} $,
das Singleton $ \{c\} $,
die Menge $ \{a, c\} $, deren Urbild $ \mathbb{R} \setminus \{0\} $ ist.

Wie in jeder Topologie sind auch hier die leere Menge und die Gesamtmenge offen:

$ \{a, b, c\} $, da ihr Urbild ganz $ \mathbb{R} $ ist,
$ \emptyset $, da ihr Urbild leer ist.

Das Singleton $ \{b\} $ ist hingegen nicht offen, da sein Urbild $ \{0\} $ kein offenes Teilset von $ \mathbb{R} $ darstellt.

Damit bestehen die offenen Mengen der Quotiententopologie auf $ \{a, b, c\} $ genau aus $ \emptyset $, $ \{a\} $, $ \{c\} $, $ \{a, c\} $ und $ \{a, b, c\} $.

Der Punkt $ b $, der dem Ursprung entspricht, besitzt kein nichttriviales offenes Umfeld. Er nimmt damit eine besondere Stellung im Quotientenraum ein, da er keine lokale Offenheitsstruktur aufweist.

Eigenschaften der Quotiententopologie

Zum Abschluss fassen wir die wichtigsten Eigenschaften der Quotiententopologie übersichtlich zusammen:

Leere Menge und Gesamtmenge sind stets offen
In jeder Quotiententopologie sind $ \emptyset $ und der gesamte Raum $ A $ per Definition offen.
- Urbild der leeren Menge
  $ p^{-1}(\emptyset) = \emptyset $, und diese Menge ist in jedem topologischen Raum offen.
- Urbild der Gesamtmenge
  $ p^{-1}(A) = X $, also der gesamte Ausgangsraum, der ebenfalls offen ist.
Anmerkung : Die trivialen Mengen behalten ihren Status als offen auch in der Quotiententopologie.
Beliebige Vereinigungen offener Mengen
Sind alle $ U_i $ offen in $ A $, so ist auch ihre Vereinigung offen, denn $$ p^{-1}\!\left( \bigcup U_i \right) = \bigcup p^{-1}(U_i) $$ ist offen in $ X $.
Endliche Schnitte offener Mengen
Sind die $ U_i $ offen in $ A $, so ist auch ihr endlicher Schnitt offen, da $$ p^{-1}\!\left( \bigcap U_i \right) = \bigcap p^{-1}(U_i) $$ offen in $ X $ ist.

Diese Eigenschaften bilden das formale Fundament zum Verständnis von Struktur und Verhalten von Quotientenräumen.