Fixpunkte in der Topologie
In der Topologie bezeichnet man als Fixpunkt einen Wert, der bei Anwendung einer Funktion unverändert bleibt.
Formal gilt: Für eine Funktion f(x) heißt p ein Fixpunkt, wenn f(p) = p erfüllt ist. Mit anderen Worten: Der Funktionswert fällt mit dem Ausgangswert zusammen, sobald die Funktion an der Stelle p ausgewertet wird.
$$ f(p) = p $$
Man kann sich das anschaulich an einer Drehung um einen festen Punkt P verdeutlichen.
Die Drehung verändert die Koordinaten sämtlicher Punkte des Objekts im Raum - nur der Punkt P bleibt unverändert.
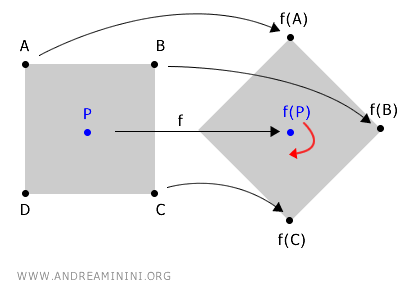
In diesem Fall fungiert das Rotationszentrum P als Fixpunkt, da seine Koordinaten unter der Abbildung f(P) unverändert bleiben.
$$ f(P) \longrightarrow P $$
Fixpunkte spielen eine grundlegende Rolle in vielen Teilgebieten und Anwendungen der Mathematik, etwa in der numerischen Analysis, der Spieltheorie oder der Wirtschaftswissenschaft.
Ein besonders bedeutendes Resultat in der Topologie ist der Brouwersche Fixpunktsatz.
Ein praktisches Beispiel
Betrachten wir die Funktion f(x) = sin(x) im abgeschlossenen Intervall [0, 2π].
$$ f(x) = \sin(x) $$
Für p = 0 ist der Fixpunkt sofort ersichtlich, da sin(0) = 0 gilt.
$$ \sin(0) = 0 $$
Hier stimmt der Funktionswert exakt mit dem Argument überein.
Beispiel 2
Nun betrachten wir die Funktion f(x) = cos(x) im selben Intervall [0, 2π].
$$ f(x) = \cos(x) $$
In diesem Fall ist x = 0 kein Fixpunkt, da cos(0) = 1 gilt - der Eingabewert unterscheidet sich also vom Ausgabewert.
Der Fixpunkt der Funktion f(x) = cos(x) liegt näherungsweise bei x = 0,73908513.
$$ \cos(0.73908513) = 0.73908513 $$
Somit gilt: cos(0.73908513) stimmt nahezu exakt mit 0.73908513 überein.
Der Brouwersche Fixpunktsatz
Der Satz lautet:
Jede stetige Abbildung eines kompakten, konvexen Teilraums im n-dimensionalen Raum besitzt mindestens einen Fixpunkt.
Es handelt sich um einen reinen Existenzsatz: Er garantiert das Vorhandensein mindestens eines Fixpunkts, ohne jedoch dessen genaue Lage zu bestimmen.
Dieses Prinzip hat weitreichende Konsequenzen, insbesondere beim Nachweis der Existenz von Gleichgewichtszuständen in dynamischen Systemen und ökonomischen Modellen.
Und so weiter.